Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 1.Exercício - Ex. 1

Mostre que, se , então e são de mesmo comprimento, mesma direção e sentido contrário.

Passo 1

Não fugiremos da abordagem do livro, com isso não usaremos demonstrações muito pesadas! Apenas utilizaremos o conceito de segmentos orientados para resolver essa questão!

Poderemos desenhar, como o livro pede, nos foi dado os pontos e a ordem deles!

Passo 2

Vamos lá então desenhar esses segmentos orientados, com valores genéricos!

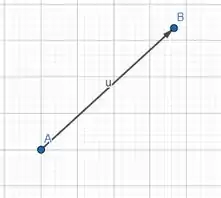
Desenhamos

Agora desenharemos .

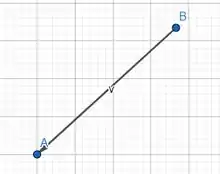
Passo 3

Vamos tirar as informações dos desenhos!

Os segmentos orientados tem o mesmo comprimento?

Sim, quaisquer segmentos que você desenhe sempre terá o mesmo tamanho!

Os segmentos orientados tem a mesma direção?

Sim!! Os segmentos são coincidentes, se você colocar um desenho sobre o outro verá que os segmentos ficarão um em cima do outro!! Segmentos orientados coincidentes tem a mesma direção!

Os segmentos tem sentidos opostos?

Um método bom de visualizar se dois segmentos coincidentes, e só coincidentes hein! Tem sentidos opostos é olhar a extremidade de ambos!

A extremidade do coincide com o de ??

Nãoo! Então eles são segmentos de sentidos contrários!

Resposta

Vide o passo a passo.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Verificar se são unitários os seguintes vetores: u → = 1,1 , 1e v → = 1 6 ,- 2 6 , 1 6

Seja o vetor v → = m + 7 i → + m + 2 j → + 5 k → . Calcular m para que v → = 38 .

A B C D é um trapézio, A B → = a → ,D C → = 2 a → e D A → = b → . O ponto E é tal que B E → = 1 3 B C → . Escreva A C → e D E → em função de a → e b → .

São dados O A → = a → , O B → = b → ,O C → = c → ,A P → = 1 3 c → ,B Q → = 4 5 a → . Escreva P Q → em função de a → ,b → e c → .

Na figura, todos os paralelogramos menores são congruentes. Sendo A D → = x →eA K → = y → , escreva os vetores G J → ,R Q → ,S I → ,H C → ,A N → ,K D → ,P H → ,A T →eO C → em função de x → e y → .