Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 1.Exercício - Ex. 4
4. Prove que:
(a)
(b)
Passo 1
Até a questão anterior, falavámos de segmentos orientados, agora falamos de vetor. Em questão de demonstração, não há muita diferença, desenharemos os vetores e procuraremos as relações que são pedidas.
Pega um conjunto de vários segmentos orientados equipolentes, esse conjunto é chamado de vetor!
Passo 2
Nesse passo 2, faremos a letra , vamos utilizar vetores genéricos desenhando os vetores e . Eles são iguais, ou seja, tem de ter mesmo comprimento, mesma direção e mesmo sentido. Desenhando:
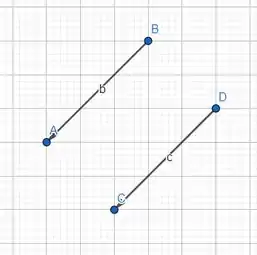
Agora desenharemos e veremos se são iguais os dois vetores.
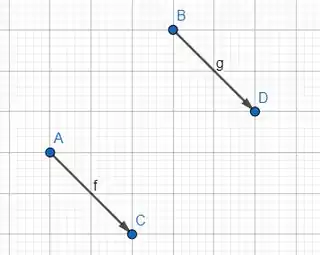
Esses dois vetores tem mesmo módulo, mesma direção e mesmo sentido! Então são iguais conforme o exercício pedia!
Passo 3
Agora vamos para a letra b), faremos do mesmo modo que fizemos a letra a). Desenharemos , sabendo que eles são iguais, então tem mesmo módulo, mesma direção e mesmo sentido.
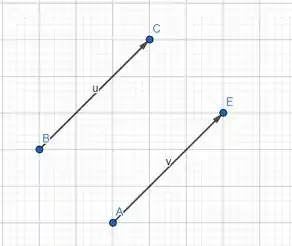
A partir desse desenho traçaremos .
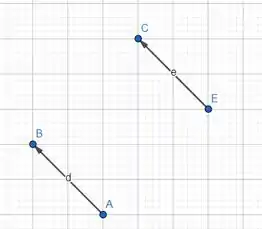
O que esses vetores têm em comum?
Ora, tem mesmo módulo (comprimento), mesmo sentido e mesma direção. Então podemos afirmar que esses dois vetores são iguais.
Resposta
Ei, a resposta está no passo a passo :)