Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 43
Prove que as diagonais de um losango estão contidas nas bissetrizes internas dos ângulos internos.
Passo 1
Queremos provar que as diagonais de um losango estão contidas nas bissetrizes internas dos ângulos internos. Para isso, vamos visualizar primeiro um paralelogramo:
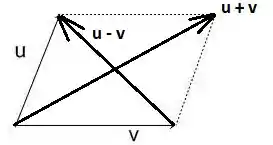
Se o paralelogramo é um losango, então
Para que a diagonal seja bissetriz, o ângulo entre e deve ser igual ao ângulo entre e . Para isso, vamos calcular o cosseno desses ângulos!
Passo 2
Para o ângulo entre e :
Assim,
Analogamente, para o ângulo entre e :
O que temos que fazer é mostrar que essas duas expressões são iguais!
Passo 3
Como o paralelogramo do caso é um losango, sabemos que . Assim,
Portanto,
Era isso que queríamos mostrar: a diagonal do losango é paralela à bissetriz do ângulo interno!
Resposta
Demonstração.