Nos casos em que a matriz dada é ortogonal, calcule sua inversa.
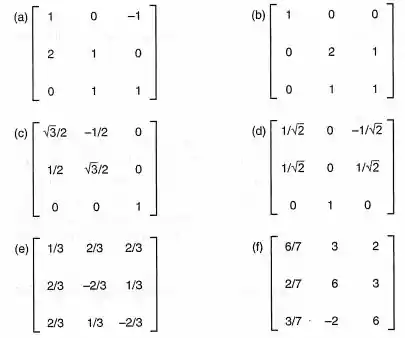
Passo 1
O problema pede para identificarmos quais matrizes são ortogonais e assim calcular sua inversa. Nesse primeiro passo vamos cuidar da identificação.
Para que uma matriz seja ortogonal, suas colunas devem ser as coordenadas de uma base ortonormal. Assim, a primeira coisa que vamos verificar é se os vetores colunas tem norma .
Olhando para a primeira coluna do item (a) ou para a segunda do item (b), vemos que essas matrizes já não são ortogonais. O mesmo ocorre na segunda coluna do item (f), pois ela não é normalizada. Sobraram (c), (d) e (e). Resta ver se as colunas são ortogonais entre si.
Na matriz (c), vemos que o produto escalar entre as colunas é sempre nulo, de modo que ela é ortogonal. O mesmo ocorre na (d) e na (e). Assim, as matrizes que são ortogonais são (c), (d) e (e).
Passo 2
Achar a inversa de matrizes ortogonais é muito fácil, pois ela é igual a sua trasposta. Assim, basta inverter linha com coluna. No item (c),
Já no item (d),
Passo 3
Por fim, a do item (e):