Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 41
Prove que:
a)
b) a soma dos quadrados dos comprimentos das diagonais de um paralelogramo é igual à soma dos quadrado dos comprimentos dos quatro lados;
c) a diagonal maior de um paralelogramo é maior do que cada um dos quatro lados.
Passo 1
O item (a) é bem simples de demonstrar e vai servir como base para os demais. Para isso, temos que usar duas relações conhecidas:
Somando as equações:
Os termos mistos se cancelam:
Passo 2
Para os itens (b) e (c), temos que visualizar o paralelogramo e suas diagonais em termos dos vetores e :
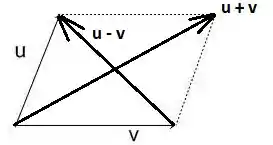
A soma dos quadrados dos comprimentos das diagonais é dada por
Já a soma dos quadrado dos comprimentos dos quatro lados é dada por
Do resultado do item (a), vemos que
Provamos o que o item pedia!
Passo 3
Para o item (c), temos que lembrar que a diagonal maior sempre corresponde ao ângulo agudo, enquanto a diagonal menor corresponde ao ângulo obtuso. Sendo assim, vamos supor que a diagonal maior é dada por , sendo o ângulo entre e agudo, como na figura.
Sabemos que
Como o ângulo entre e é agudo, sabemos que , de modo que
Assim, sabemos que
Ou ainda,
Assim, vemos que a diagonal maior é maior que cada um dos lados do paralelogramo!
Resposta
Demonstração.