Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 11.Exercício - Ex. 11
a) Prove que, se , então . Conclua que, na Definição 11-1, a condição (), pode ser substituída por
b) Calcule a norma de , sabendo que , e .
c) Em relação a uma base ortonormal, e . Calcule .
d) O lado do triângulo equilátero mede . Calcule em função de .
e) Seja um tetraedro regular de aresta unitária. Calcule .
Passo 1
A demonstração do item (a) é bem simples e seu resultado vai ser usado em todos os demais itens. Sabemos que
Assim,
Mas o termo entre parênteses é o produto escalar:
Portanto,
Mas da definição da norma de um produto vetorial:
Com isso,
Essa fórmula é um jeito simples de calcular a norma de um produto vetorial entre dois vetores se conhecermos o produto escalar! Nos próximos itens vamos usar bastante ela!
Passo 2
No item (b) temos , e . Usando a fórmula do item (a):
Portanto,
Passo 3
No item (c), temos e , de modo que
Já o produto escalar:
Assim,
Portanto,
Passo 4
No item (d) temos dois vetores com norma que forma :
Assim,
Portanto,
Passo 5
Por fim, vamos ao item (e), em que temos um tetraedro regular .
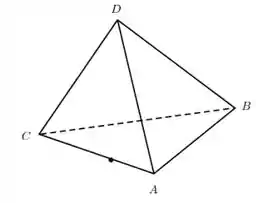
Vamos calcular primeiro o produto escalar . Para isso, escrevemos
Portanto,
Mas note que tanto e como e são lados de uma mesma face do tetraedro, de modo que os dois produtos escalar são iguais:
Portanto,
Logo,
Assim,