Prove que o lugar geométrico dos pontos de que equidistam de três pontos dados, e é:

a) uma reta perpendicular ao plano , se os três pontos não são colineares;

b) o conjunto vazio, se e são colineares e ;

c) um plano perpendicular à reta que contém e , se (apenas) dois desses pontos coincidem;

d) o espaço , se .

a) Nesse caso, temos algo assim:

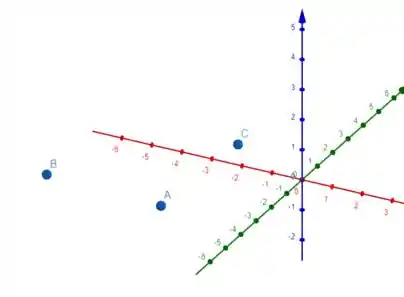
Os vetores normais e dos planos transversais são LI, pois os pontos não são colineares, portanto, os planos são transversais e se interceptam em uma reta.

Essa reta, que representa o lugar geométrico , vai ter vetor diretor paralelo a , e, portanto, por definição de produto vetorial, é perpendicular ao plano .

Interessante lembrarmos que essa reta vai passar no circuncentro do triângulo .

b) Agora, como os pontos são colineares, temos algo assim:

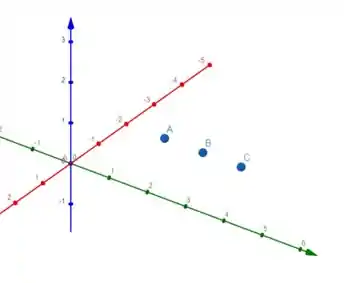
Nesse caso, com os pontos sendo colineares, os planos mediadores são paralelos, pois e são LD (já que são paralelos), certo? Além disso, como o ponto médio de só pertence a um dos planos e o ponto médio de pertence ao outro, os planos são distintos.

Sabemos que dois planos paralelos distintos não possuem intersecção, e como essa intersecção seria dada pelo lugar geométrico que queremos, não existe nesse caso ;)

c) Vamos supor que :

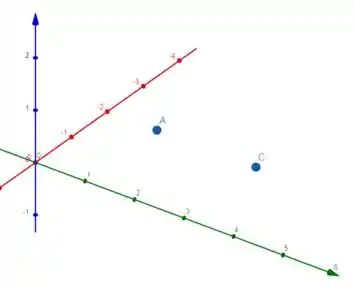
Nesse caso, os planos mediadores são iguais, porque o vetor normal é igual ao vetor normal .

A intersecção entre dois planos iguais é o próprio plano, certo? E como (ou ) são os vetores normais desse plano, ele é perpendicular à reta que contém e .

d) Se , é como se tivéssemos apenas um ponto, apenas um lugar geométrico para representar e .

Por geometria, sabemos que qualquer ponto, reta, plano, enfim hehe qualquer lugar geométrico terá a mesma distância até e , pois eles estão no mesmo lugar. Então, o lugar geométrico é o próprio .