Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 1.Problemas - Ex. 8

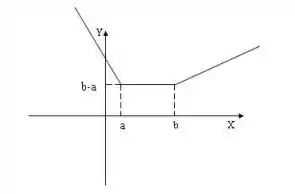
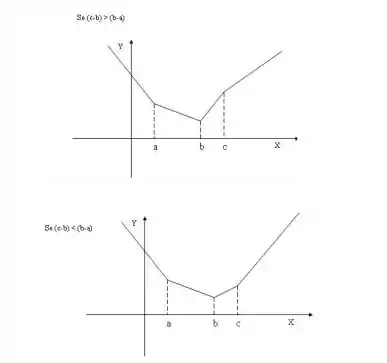
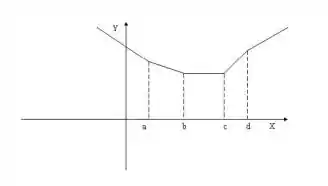
Sejam A, B, C, D pontos dispostos nesta ordem sobre um eixo E. Esboce os gráficos das funções φ , f , g : E → R , dadas por:

φ X = d X , A + d X , B ,

φ X = d X , A + d X , B + d X , C ,

φ X = d X , A + d X , B + d X , C + d X , D .

Passo 1

Fala aí pessoal tudo blz?

Nessa questão sabendo que A, B, C, D pontos dispostos nesta ordem sobre um eixo E. Esboce os gráficos das funções φ , f , g : E → R , dadas por:

φ X = d X , A + d X , B ,

φ X = d X , A + d X , B + d X , C ,

φ X = d X , A + d X , B + d X , C + d X , D .

Pode ficar calminho que você vai entender legal, só confia.

Passo 2

Sabendo que,

X ↔ x ,   A ↔ a , B ↔ b ,   C ↔ c       e     D ↔ d

Como a < b < c < d , temos

φ X = x - a + x - b = a + b - 2 x ; s e   x ≤ a b - a ; s e   a ≤ x ≤ b 2 x - b + a ; s e   x ≥ b

Considere a > 0

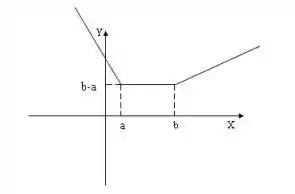
Passo 3

Para,

f X = x - a + x - b + x - c = a + b + c - 3 x ; s e   x ≤ a b - a + c - x ; s e   a ≤ x ≤ b x - b + a + c ; s e   b ≤ x ≤ c 3 x - a + b + c ; s e   c ≤ x

Considerando a > 0

E por fim para,

g X = x - a + x - b + x - c + x - d = a + b + c + d - 4 x ; s e   x ≤ a b - a + c + d - 2 x ; s e   a ≤ x ≤ b - b + a + c + d ; s e   b ≤ x ≤ c 2 x - a + b + c + d ; s e   c ≤ x ≤ d 4 x - a + b + c + d ; s e   d ≤ x

Considerando a > 0

Espero ter ajudado, e até a próxima.

Resposta

Exercícios de Livros Relacionados

Obtenha os pontos da reta r que equidistam de A e B e comente as peculiaridades geométricas de cada caso.a) r : x - 1 = 2 y = zA = 1 ,1 ,0B = ( 0 ,1 ,1 )
Obtenha equações do lugar geométrico dos pontos de E ³ ³ que equidistam de A , B e C e determine as coordenadas do circuncentro do triângulo A B C , nos casos:a) A = 0 ,2 ,1 B = 2 ,2 ,- 1 C = ( - 2 ,0
Obtenha equações do lugar geométrico dos pontos de E ³ ³ que equidistam de A , B e C e determine as coordenadas do circuncentro do triângulo A B C , nos casos:b) A = 3 ,0 ,1 B = 2 ,1 ,0 C = ( 4 ,- 1 ,
Prove que o lugar geométrico dos pontos de E ³ ³ que equidistam de três pontos dados, A ,B e C é:a) uma reta perpendicular ao plano A B C , se os três pontos não são colineares;b) o conjunto vazio, se
Sejam p um número real positivo, A e B dois pontos tais que d A , B = p , e n , um número real qualquer. Prove que o lugar geométrico dos pontos X de E 3 tais que d X , A 2 - d X , B 2 = n é um plano