Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 4.Problemas Propostos - Ex. 13e
Represente graficamente as retas cujas equações são:
e)
Passo 1
No caso, temos equações planares da reta, ou seja, a reta que queremos é a intersecção entre os dois planos dados hehe
Temos
Então, nossa reta tem o formato
Transformando em um parâmetro e colocando em evidência, temos
Então, nossa reta passa pelo ponto e tem vetor diretor :)
Passo 2
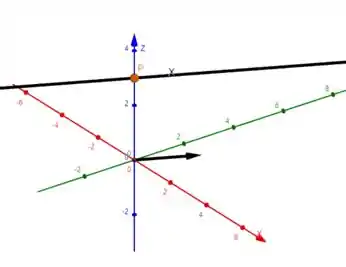
Como o nosso ponto tem coordenadas , vamos localizá-las no espaço, encontrando o ponto da imagem:
Agora para encontrarmos o vetor diretor, vamos desenhar um segmento da origem até o ponto , tendo o vetor da imagem abaixo:
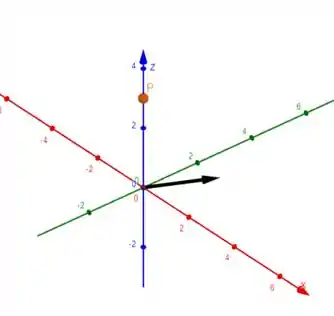
Então, para encontrarmos a nossa reta, vamos desenhar um segmento que passa por e está na direção do vetor preto da imagem acima, e aí temos
Resposta
Exercícios de Livros Relacionados
19. Determinar as equações paramétricas e representar graficamente a reta que passa por:e) A 3 ,- 1 ,3 e B 3 ,3 ,4 .
Escrever as equações paramétricas das retas que passam pelo ponto A 4 ,- 5 ,3 e são, respectivamente, paralelas aos eixos O x , O y e O z .
Determinar, caso exista, o ponto de interseção das retas r 1 e r 2 : r 1 : y = 2 x - 3 z = - x + 5e r 2 : y = - 3 x + 7 z = x + 1
Determinar, caso exista, o ponto de interseção das retas r 1 e r 2 : r 1 : x - 3 2 = y + 1 - 3 = z - 2 4 e r 2 : x = - 1 + t y = 4 - t z = - 8 + 3 t
Determinar, caso exista, o ponto de interseção das retas r 1 e r 2 : r 1 : y = 2 x - 3 z = - x + 10e r 2 : y = 3 x + 4 z = - 2 x - 1