Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 8.Problemas - Ex. 2
A reta definida pelas equações paramétricas , forma um ângulo agudo com reta . Determine .
Passo 1
Faaaala, galeeera!
Dada as equações e , vamos obter a equação reduzida.
Isolando em , temos:
Substituindo em , temos:
Então devemos obter os coeficientes angular de cada reta.
Temos e .
Para obter o valor do ângulo devemos utilizar a seguinte fórmula:
Abaixo temos a representação do problema.
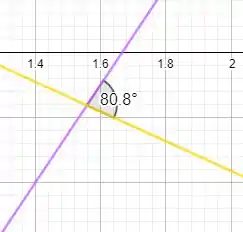
Questão finalizada! : )
Resposta
Exercícios de Livros Relacionados
Obtenha uma equação vetorial da reta que contém o ponto P = ( 0 ,2 ,1 ) e forma ângulos congruentes com as retas r : X = 0 ,0 ,0 + λ ( 1 ,2 ,2 ) , s : X = 1 ,2 ,3 + λ ( 0 ,3 ,0 ) e t : X = 1 ,2 ,0 + λ
Obtenha uma equação vetorial da reta que forma ângulos congruentes com os eixos coordenados e é concorrente com r : 2 x - 2 = 3 y - 3 = - 2 z e s : - 1,1 , 0 + λ 5,3 , 1 .
O triângulo ABC é retângulo em B e está contido no plano π 1 : x + y + z = 1 . O cateto BC está contido no plano π 2 : x - 2 y - 2 z = 0 e o ângulo C ^ mede 30°. Dado A = 0,1 , 0 , determine B e C e c
15. Determinar o valor de n para que seja de 30 ° o ângulo entre as retas r : x - 2 4 = y + 4 5 = z 3 e s : y = n x + 5 z = 2 x - 2
14. Determinar o ângulo entre as seguintes restas:(a) r : x = - 2 - 2 t y = 2 t z = 3 - 4 t e s : x 4 = y + 6 2 = z - 1 2 (b) r :y = - 2 x - 1 z = x + 2 e s : y 3 = z + 1 - 3 ; x = 2 (c) r : x = 1 + 2