Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 47c
As retas que contêm alturas de um triângulo são concorrentes num ponto, chamado ortocentro do triângulo. (Este resultado foi objeto do Exercício 5-21. Sua verificação, com o auxílio da Relação de Euler, fica muito simplificada).
Passo 1
Bora lá!
Para confirmamos a existência do ortocentro de um triângulo, primeiramente, vamos considerar os pontos A, B, C e D dispostos como mostra a nossa figura:
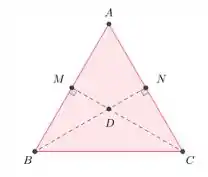
Notem, que no nosso triângulo, há apenas as alturas relativas à dois vértices, B e C, e o ponto de intersecção destas, D.
Dessa forma, devemos mostrar que, ao traçarmos a terceira altura, sendo esta relativa ao vértice A, teremos novamente, a intersecção com o ponto D, beleza?
Então, partiu.
Passo 2
Para tanto, se nós considerarmos os lados desse triângulo como vetores, podemos notar que, obrigatoriamente, seus ponto devem obedecer a Relação de Euclides da letra (a). Dessa forma, escreveremos tal relação, levando em consideração que, devido aos ângulos retos, e . Temos, então:
Passo 3
Portanto, concluímos que a altura relativa ao vértice A intercepta, de fato, o ponto D, o ortocentro do triângulo. 😉
Resposta
Ei, a resposta está no passo a passo :)