Seja ABCD um retangulo de diagonal BD. Prove que , qualquer que seja o ponto P.
Passo 1
Bora lá!
Inicialmente, vamos esboçar o nosso retângulo
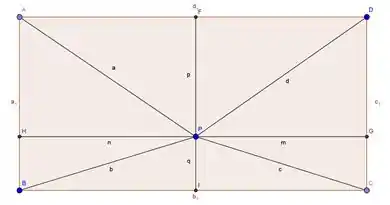
Passo 2
Agora, podemos estabeler quatro relações, usando o nosso famoso e salvador Teorema de Pitágoras. Podemos soma-las duas a duas, a fim de verificar a igualdade.
Desse modo, provamos que , qualquer que seja o ponto P.
Resposta
Ei, a resposta está no passo a passo :)