Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 24b
Sejam e duas retas concorrentes em B, tangentes à circunferência de centro A e raio , (Figura 5-10). Com centro em um ponto P da semi-reta de origem B que contém A, traça-se a circunferência de raio (menor que ), tangente às retas e . Sejam e duas retas tangentes à segunda circunferência, concorrentes em R. Com centro em um ponto Q da semi-reta de origem R que contém P, traça-se a circunferência de raio (menor que ), tangente às retas e . Sejam e as retas tangentes comuns à primeira e à terceira circunferências que tenham em comum um ponto C da reta AQ, exterior ao segmento AQ. Prove que B, C e R são colineares..
Passo 1
Bora lá!
Na figura abaixo estão representados, além dos pontos originais dados no problema, os pontos de tangência das retas com as circunferências. Os segmentos BC e CR foram suprimidos propositalmente para que não haja a falsa impressão de que já a princípio os pontos B, C e R são colineares. Os segmentos coloridos unem o centro da circunferência aos seus pontos de tangência com as retas.
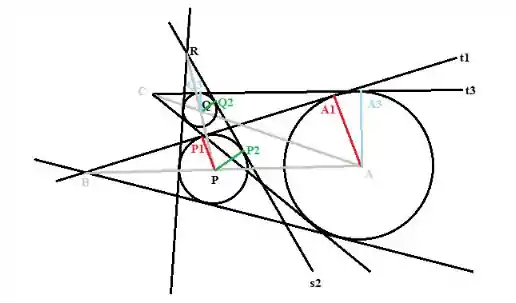
Notem que:
Os segmentos fazem um ângulo de 90° com as respectivas retas tangentes;
Dois segmentos de mesma cor são perpendiculares à mesma reta e, por isso, são paralelos entre si.
Passo 2
Levando-se em consideração estas observações feitas, podemos utilizar o Teorema de Tales para estabelecer as seguintes relações de semelhança:
Agora vem o bizu... prestem atenção nesse detalhe.
Ocorre que cada um dos segmentos coloridos tem o comprimento do raio de uma circunferência, certo? Vamos denotar os raios das circunferências de centro A, P e Q respectivamente por Ra, Rb e Rq, ok? Dessa forma, podemos simplificar as equações acima:
Passo 3
Agora vem o nosso famoso “pulo do gato”, por um motivo que ficará mais claro já já, podemos renomear as razões entre os raios nas equações acima da seguinte forma:
de maneira que
Utilizando estas definições e notando que os segmentos em cada uma das equações (1), (2) e (3) são paralelos, estas 3 relações podem ser reescritas em forma vetorial da seguinte maneira:
Tarãmm, essas eram relações de semelhando da letra (a).
Passo 4
Finalmente, conforme já demostrado na letra (a), está é a condição para que os pontos B, C e R sejam colineares.
Resposta
Ei, a resposta está no passo a passo :)