Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 4.Exercícios Propostos - Ex. 28
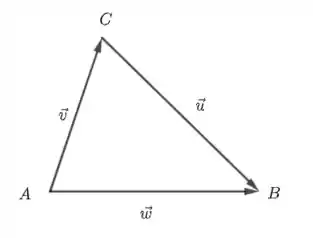
Já sabemos que a área do triângulo da figura é . A área do triângulo também é dada por ? Justifique sua resposta (a) geometricamente; (b) algebricamente.
Passo 1
Fala, pessoal! Essa questão é daquelas que é tão simples que às vezes a gente não sabe como demonstrar. Mas calma, com um pouco de paciência vamos conseguir.
- geometricamente, podemos considerar a largura do triângulo como representada por e a altura representada pela projeção de numa direção perpendicular a . Essa projeção, em módulo, é dada por onde é o ângulo entre . Assim, a área do triângulo fica dada por
Passo 2
b) Algebricamente, temos que notar que
Então, vamos substituir isso na segunda fórmula para a área
Opa! Conseguimos mostrar que a área também pode ser dada por .
Resposta
Veja a resolução acima.
Exercícios de Livros Relacionados
Sabendo que u → = 6 ,v → = 4 e 30 ° o ângulo entre u → e v → , calcular:b) a área do paralelogramo determinado por u → e ( - v → ) ;
Dados os vetores u → = ( 3 , - 1 ,2 ) e v → = ( - 2 ,2 ,1 ) , calcular:a) a área do paralelogramo determinado por u → e v → ;
Dados os vetores u → = ( 3 , - 1 ,2 ) e v → = ( - 2 ,2 ,1 ) , calcular:b) a altura do paralelogramo relativa à base definida pelo vetor v → .
Sabendo que u → = 6 ,v → = 4 e 30 ° o ângulo entre u → e v → , calcular:a) a área do triangulo determinado por u → e v → ;
Calcular a distância do ponto P ( 4 ,3 ,3 ) à reta que passa por A ( 1 ,2 , - 1 ) e B ( 3 ,1 ,1 ) .