Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 3.Problemas propostos - Ex. 21a
Sabendo que e o ângulo entre e , calcular:
a) a área do triangulo determinado por e ;
Passo 1
Primeiro, vamos fazer um esboço do nosso problema:
A metade da área do paralelogramo será a área do triângulo determinado pelos vetores.
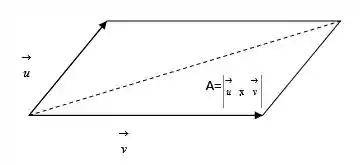
Passo 2
Sabemos que , certo? Então, substituindo os valores dados, temos:
Passo 3
Estamos quase lá. Como a área do triângulo é igual à metade da área do paralelogramo, temos:
Portando, a área do triângulo é igual a 6.
Resposta
Exercícios de Livros Relacionados
Mostre que 0 × a = 0 = a × 0 Para qualquer vetor a em V 3 .
Se a = 1,2 , 1 eb = ( 0,1 , 3 ) , calcule a × b e b × a .
Determine dois vetores unitários que sejam ortogonais tanto a a = ( 1 , - 1,1 ) Quanto a b = ( 0,4 , 4 )
Demonstre a Propriedade 3 do Teorema 8.
Sejam U e V vetores no espaço, com V ≠ 0 - .b) Mostre que U + V × U - V = 2 V × U .