Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 6.Exercícios Propostos - Ex. 18

São dadas três retas r , s e t : r {   x - 7 4   =   y + 2 - 2   =   z - 2 3 .

⎧ x   = 3   -   4 m

  s   ⎢ y   = 2 m

        ⎩   z   = - 1 - 3 m

e t que passa por A = ( 1 , - 1,0 ) e B =   ( 7 , - 6,7 ) .

  1. Escreva equações paramétricas da reta r e, também, da reta t .
  2. Estude a posição relativa das retas r e s . Desenhe r e s .
  3. Estude a posição relativa das retas r e t . Desenhe r e t .

Passo 1

  1. A reta s já está escrita na forma paramétrica, só precisamos então das outras duas

    2. r {   x - 7 4   =   y + 2 - 2   =   z - 2 3 = λ ⇒ x = 4 λ + 7 ,   y = - 2 λ - 2 ,   z = 3 λ + 2

    Para a reta t , vamos considerar que seu ponto inicial é dado por A = ( 1 , - 1,0 ) e que seu vetor diretor é igual a vetor

    v → t = A B → = B - A =   ( 7 , - 6,7 ) - ( 1 , - 1,0 ) = ( 6 , - 5,7 )

    Assim, as equações paramétricas da reta t serão:

    x = 6 γ + 1 ,   y = - 5 γ - 1 ,   z = 7 γ

    Passo 2

  2. Os vetores diretores das retas r e s são, respectivamente

    3. v → s = ( - 4,2 , - 3 )

    v → r = ( 4 , - 2,3 )

    Assim, vemos que v → s = - v → r de modo que as retas são paralelas. Para descobrir a posição relativa entre as duas, vamos reescrever

    x - 7 4   =   y + 2 - 2   =   z - 2 3 = λ   ( × ( - 1 ) )

    ⇒ x - 7 - 4   =   y + 2 2   =   z - 2 - 3 = - λ   ≡ λ ' + 1

    onde definimos - λ   ≡ λ ' + 1 por conveniência. Assim, as equações paramétricas da reta r se tornam:

    x = - 4 ( λ ' + 1 ) + 7 = - 4 λ ' + 3 ,

    y = 2 ( λ ' + 1 ) - 2 = 2 λ ' ,

    z = - 3 ( λ ' + 1 ) + 2 = - 3 λ ' - 1

    É fácil ver que as equações acima são idênticas a

    ⎧ x   = 3   -   4 m

      s   ⎢ y   = 2 m

            ⎩   z   = - 1 - 3 m

    Isso quer dizer que as duas retas são iguais. As duas retas, que na verdade são só uma, estão desenhadas abaixo:

    Passo 3

  3. Os vetores diretores das retas ( v → t = ( 6 , - 5,7 ) e v → r = ( 4 , - 2,3 ) ) não são paralelos. Então as retas r e t são concorrentes ou reversas. Se as retas forem concorrentes, elas têm um ponto em comum no qual

x = 6 γ + 1 = 4 λ + 7

y = - 5 γ - 1 = - 2 λ - 2

  z = 7 γ = 3 λ + 2

Assim,

x + 2 y = - 4 γ - 1 = 3

⇒ - 4 γ = 4 ⇒ γ = - 1

Logo, usando γ = - 1 na segunda equação, obtemos

- 5 γ - 1 = - 2 λ - 2 ⇒ 5 - 1 = - 2 λ - 2

⇒ 2 λ = - 2 - 4 ⇒ λ = - 3

Ok, como foi possível encontrar um m e um γ satisfazendo as equações acima, quer dizer as retas são concorrentes. Para encontrar o ponto em comum das duas, fazemos γ = - 1 na reta t ou λ = - 3 na reta r :

Reta t :

x = 6 γ + 1 = - 6 + 1 = - 5

y = - 5 γ - 1 = 5 - 1 = 4

  z = 7 γ = - 7

Logo, o ponto de encontro é ( - 5,4 , 7 )

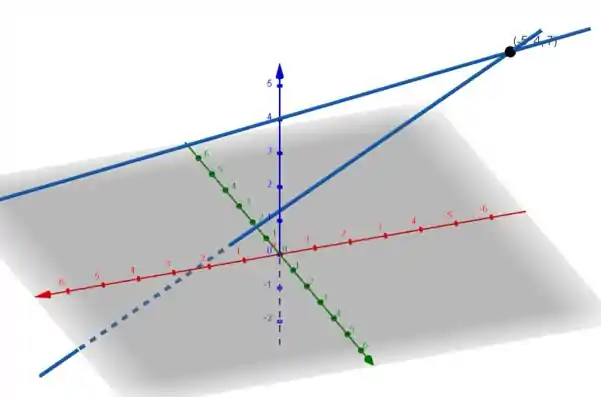
Resposta

  1. r : x = 4 λ + 7 ,   y = - 2 λ - 2 ,   z = 3 λ + 2 , t : x = 6 γ + 1 ,   y = - 5 γ - 1 ,   z = 7 γ
  2. r = s
  3. r e t são concorrentes em ( - 5,4 , 7 ) .

Exercícios de Livros Relacionados

Determine se as retas L 1 e L 2 são paralelas, reversas ou concorrentes. Se forem concorrentes, determine seu ponto de intersecção.21. L 1 : x 1 = y - 1 2 = z - 2 3 L 2 : x - 3 - 4 = y - 2 - 3 = z - 1
É dado o Δ A B C com A=( 2,3 , - 1 ) , B=( 4 , - 1,5 ) e C=( 0,3 , - 1 ) .Escreva equações das três medianas.Ache a interseção de duas delas.Mostre que a terceira mediana passa pela interseção das out
As retas ⎧x=1+ 3 α⎧ b⎢ y= 1- α ⎢ ⎩ z= - 3+ 5 α⎩ ⎧ x= 1⎧ c⎢ y= 1-2 β ⎢ ⎩z=- 3+3 β⎩ passam pelo vértice A do triângulo A B C e, respectivamente, pelos vértices B e C . Determine as coordenadas de A , B
Determine a , b , c e d para que as retas r e s coincidam, sendo: ⎧ x=1+ 4 λ⎧ r⎢ y= a- 2 λ ⎢ ⎩ z= - 1+ b λ⎩ ⎧ x= 9+2 β⎧ s⎢ y= - 1+c β ⎢ ⎩z=d+3 β⎩