Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 14.4 - Ex. 13

Seja f x ,   y = 3 x + 3 y definida na região poliedral convexa abaixo:

  1. Qual o valor máximo e mínimo de f ?
  2. Calcule os valores f ( A ) , f ( B ) e f ( P ) , onde P é um ponto no segmento A B .
  3. Use ( a ) e ( b ) para determinar os pontos onde f atinge o máximo e os pontos onde assume o mínimo.

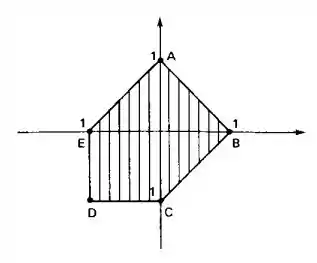
Passo 1

  1. A nossa função que queremos maximizar (e minimizar) é f x , y = 3 x + 3 y . Vamos no de sempre: a gente pega o vetor perpendicular a essa reta. Partindo da origem, ele vai estar na direção - 3 x + 3 y = 0 .

    2. Agora a gente tem que interceptar essa reta com a figura e ver onde vai bater. Bora traçar essa parada!

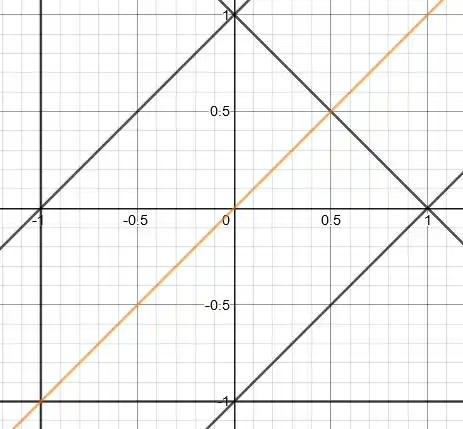
    Do desenho a gente já vê: a nossa reta bate no segmento A B e no vértice D . Bom, já dá pra ver que o ponto D vai ser um ponto de mínimo, né? A gente tem que interceptar com a reta A B então! Igualando as equações:

    - 3 x + 3 y = 0 x + y = 1

    Juntando as duas vamos obter:

    x = y = 1 2

    Então show! O máximo vai ser:

    M = f 1 2 , 1 2 = 3 2 + 3 2 = 3

    E o mínimo:

    m = f - 1 ,   - 1 = - 3 - 3 = - 6

    Passo 2

  2. Vamos calcular o valor da função pra aqueles pontos:

    3. f A = 3 0 + 3 1 = 3

    f B = 3 1 + 3 0 = 3

    E pra um ponto qualquer P na reta:

    y = - x + 1

    E aí a função vai valer:

    f P = 3 x + 3 - x + 1 = 3

    Ih, deu igual em tudo que é canto!

    Passo 3

  3. Os pontos de máximo vão ser todos os pontos da reta A B , e o ponto de mínimo vai ser só o ponto D , já que, pra A B , todos os pontos ali têm o mesmo valor da função, e pra D , se a gente aumentar um tantinho uma das componentes, já saímos do vértice e não vai ser o mínimo! Isso acontece pra A B porque a reta é perpendicular ao gradiente da função que queremos calcular!

Resposta

  1. Máximo: 3 , Mínimo: - 6 .
  2. f A = f B = f P = 3
  3. Máximo: toda a reta A B . Mínimo: vértice D .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o sistema de equações, escrevendo as matrizes ampliadas, associadas aos novos sistemas. 2 x - y + 3 z = 11 4 x - 3 y + 2 z = 0 x + y + z = 6 3 x + y + z = 4
Numa indústria química há uma caldeira cuja margem de segurança é tal que a pressão P é medida em atmosferas, e a temperatura T , medida em graus Celsius, devem ser reguladas de maneira que 10 P + T ≤
Uma máquina produz dois tipos A e B de frascos de vidro, mas não simultaneamente. Ao produzir um frasco do tipo A ela gasta 0,2 horas, e ao produzir um tipo B , gasta 0,4 horas. Sabendo que a máquina
Na definição de variedade linear em 14.2 . 1 , prove que v 0 ∈ A . O vetor v 0 é único? W é único? Interprete geometricamente.
Para o sistema linear dado, encontre todos os valores de a para os quais o sistema não tem solução, tem solução única e tem infinitas soluções: x + 2 y + z = 3 x + y - z = 2 x + y + a 2 - 5 z = a