Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 14.4 - Ex. 10
Uma máquina produz dois tipos e de frascos de vidro, mas não simultaneamente. Ao produzir um frasco do tipo ela gasta horas, e ao produzir um tipo , gasta horas. Sabendo que a máquina pod trabalhar no máximo horas por dia e que o fabricante tem um lucro de com um frasco tipo e com um frasco tipo , quantos frascos de cada tipo devem ser produzidos para que o lucro seja máximo?
Passo 1
Aqui vamos dizer que é a quantidade de frascos do tipo e os frascos do tipo , show? E aí, o tempo gasto por cada produção de é horas, e de , horas. O lucro com é de , e com de , certo? Já temos tudo pra escrever as desigualdades:
E o que a gente quer? A gente quer maximizar a função . Estamos juntos?
Passo 2
Beleza, já vimos como é que a gente faz isso na teoria. Bora esboçar essa região aí! Traçando a inequação da terceira linha, vamos ficar com esse gráfico:
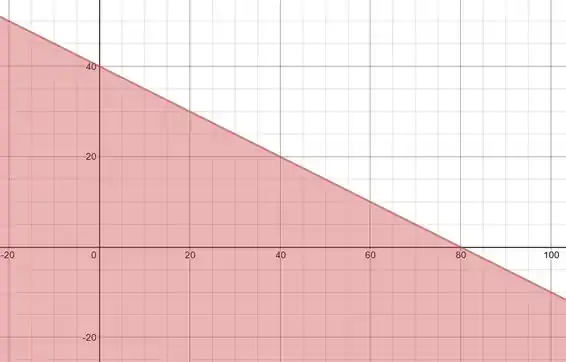
Como a gente quer o e o maiores ou iguais a zero, vamos ficar só com o triângulo acima do eixo e à direita do eixo . Beleza, como queremos maximizar , vamos pegar a reta que é perpendicular a essa função! Ela é dada por , certo? Então a reta que passa pela origem e tem essa direção é:
Interceptando essa função com a reta da bordinha da inequação, vai ficar:
Substituindo a primeira na segunda:
E aí, com isso,
Passo 3
Pronto, achamos os valores que dão o máximo que a gente queria! O lucro dessa produção vai ser: