Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 17.Problemas - Ex. 4
Segundo a Geometria Elementar, se D é um ponto do lado BC do triângulo ABC então a reta AD é bissetriz do ângulo BÂC se, e somente se, . Use este fato para mostrar que a tangente á hipérbole no ponto é a bissetriz do ângulo , onde F e F’ são os focos da hipérbole
Passo 1
Falaaa, blz??? Bom, para começar essa questão vamos usar o desenho para nos ajudar a entender como aplicar tal teorema:
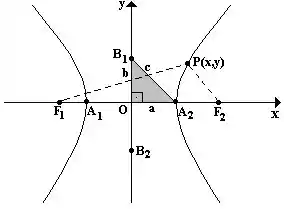
Pela equação da nossa hipérbole, temos que:
Ou seja, como queremos mostrar que a tangente que passa no ponto P, dado no enunciado, é a bissetriz do ângulo FPF’, o que queremos na verdade é achar um ponto D no segmento FF’ que pertença à reta tangente e checar se esse segmento PD é bissetriz do ângulo FPF’
Passo 2
Vamos usar a informação da questão 2 para nos ajudar, pois precisamos achar o ponto no segmento FF’ (no desenho que pertence á reta tangente em P
Com isso, temos que:
Como queremos um ponto D no segmento FF’, ele tem y=0, logo:
Ou seja, temos algo do tipo:
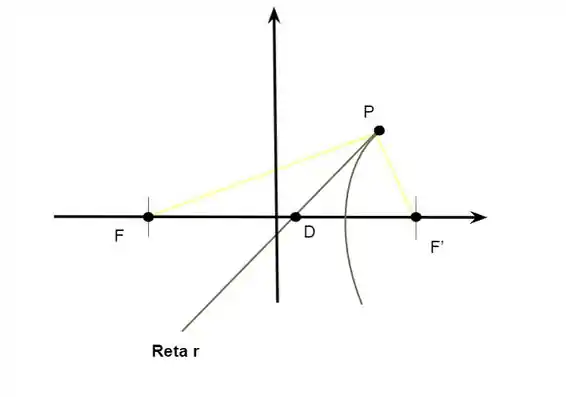
Com:
Agora vamos focar no triângulo FPF’
Passo 3
Queremos mostrar que:
Se isso ocorrer, temos que de fato a tangente é bissetriz.
Colocando na equação:
Queremos ver se isso é verdade.
Outro:
Agora fica bem mais fácil enxergar que ambos são iguais, logo, como a igualdade é verdadeira, provamos que a tangente é também bissetriz.
Resposta
Ei, a resposta está no passo a passo :)