Seja . Fazer um gráfico de um vetor genérico do domínio e de sua imagem sob a transformação linear dada por:
Passo 1
O problema fornece uma transformação linear de em e pede para representarmos ela no plano cartesiano.
Considerando o vetor , se aplicar a transformação sobre ela, temos que
A coordenada não foi alterada pela transformação, porém na direção ela foi duplicada!
Passo 2
Na figura a seguir esboçamos (em vermelho) e (em azul):
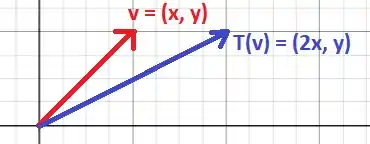
Resposta
Desenho