Seja f uma função que faz correspondente a cada par de vetores v = ( a 1 ,b 1 ) , w = ( a 2 ,b 2 ) um numero real f v , w . (Noutras palavras tem-se uma função f :R 2xR 2 → R ). Suponha que f tem as seguintes propriedades para quaisquer v , v ' ,wϵ R 2 e αϵR ;d) v = ( 1 , 0 ) e w = ( 0 , 1 ) , então f v , w = 1 Prove que f v , w = a 1 b 2 - a 2 b 1

Então, podemos concluir, a relação da dada na questão satisfaz e como também o determinante é igual 1. 1 0 0 1 = 1 a 1b 1 a 2 b 2 = - a 2 b 1 + a 1 b 2 Espero que ajudem nos estudos, até próxima

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 35.Problemas - Ex. 3d

Seja f uma função que faz correspondente a cada par de vetores , um numero real (Noutras palavras tem-se uma função ). Suponha que f tem as seguintes propriedades para quaisquer , e ;

d) e , então

Prove que

Passo 1

Fala galerinha , vamos resolver mais uma questão do nosso livro de Geometria analítica e Álgebra Linear !!!

Primeiramente com valores dados em cada um dos vetores, vamos substituir na matriz de forma que obedeça a função ,

Vamos então ao próximo passo...

Passo 2

O próximo passo será, provar a relação . Para isso será substituído na matriz com os vetores e

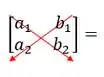
Resposta

Então, podemos concluir, a relação da dada na questão satisfaz e como também o determinante é igual 1.

Espero que ajudem nos estudos, até próxima

Exercícios de Livros Relacionados

1. Dado os vetores vec u = 2 vec i - 3 vec j , vec v = vec i - vec j e vec w = - 2 vec i + vec j , determinar:c) vec v - vec u + 2 vec w

1. A figura 1.29 apresenta o losango E F G H inscrito no retângulo A B C D , sendo O o ponto de intersecção das diagonais desse losango. Decidir se é verdadeira ou falsa cada uma das seguintes afirmaç

1. Dado os vetores vec u = 2 vec i - 3 vec j , vec v = vec i - vec j e vec w = - 2 vec i + vec j , determinar:a) 2 vec u - vec v