Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 3
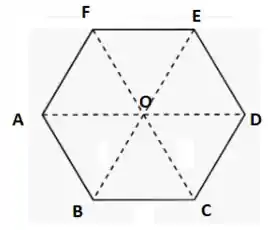
Seja um hexágono regular de centro , como o da Figura 2-10. Obtenha as seguintes medidas angulares em graus:
a)
b)
c)
d)
Passo 1
Consideremos o hexágono regula da figura a seguir:
No item (a) temos os vetores e :
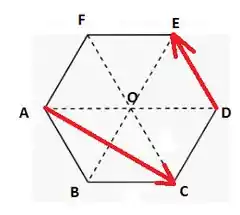
Lembre-se que o ângulo de cada triângulo interno é .
Reposicionando o vetor :
O ângulo entre eles será
Passo 2
Para o item (b), traçamos a soma e o vetor :
O ângulo é claramente um ângulo reto:
Passo 3
Agora no item (c), fazemos a soma e colocamos também o vetor :
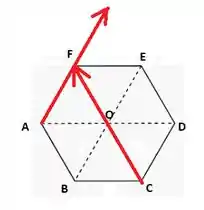
O ângulo entre eles é
Passo 4
Por fim, no item (d), temos que
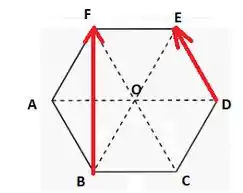
Reposicionando os vetores:
Assim,
Resposta
Exercícios de Livros Relacionados
Determine o vetor projeção e a projeção escalar de b sobre a . a = ( 1,2 ) , b = ( - 4,1 )
Encontre o trabalho feito por uma força F = 8 i - 6 j + 9 k Que move um objeto do ponto ( 0,10,8 ) para o ponto ( 6,12,20 ) ao longo de uma reta. A distancia é medida em metros e a força em Newtons.
Seuponha que a e b sejam vetores não nulos.Sob quais circunstancias c o m p ab = c o m p ba ?Sob quais circunstancias p r o j ab = p r o j ba ?
Determine o vetor projeção e a projeção escalar de b sobre a . a =3 , - 4 b =5,0
Para os vetores do Exercício 36, determine p e r p a b e ilustre esboçando os vetores a ,b ,p r o j a b e p e r p a b . a = ( 1,2 ) b = ( - 4,1 )