Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 35.Problemas - Ex. 6

Seja m ' uma matriz 3x3 obtida de m pelo processo de escalonamento. Prove que det[ m ' ] = ( - 1 ) i det ⁡ m , onde i é o número de vezes em eu foi feita alguma troca de posição entre linhas.

Passo 1

Fala galerinha , vamos resolver mais uma questão do nosso livro de Geometria analítica e Álgebra Linear !!!

Primeiramente vamos escrever nossa matriz m e m '

m = a 1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3

m ' = a 1 ' a 2 ' a 3 ' 0 b 2 ' b 3 ' 0 0 c 3 '

Com isso em mente, vamos então ao próximo passo...

Passo 2

Este passo será encontrar o valor do   det ⁡ m  

det ⁡ m =   - a 3 b 2 c 1 - c 2 b 3 a 1 - c 3 a 2 b 1 +   a 1 b 2 c 3 + c 2 b 1 a 3 + c 1 a 2 b 3

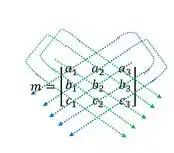
Passo 3

Agora vamos, realizar o processo de escalonamento na matriz m e encontrar quantas vez é preciso mudar as linhas de posição

m = a 1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3               L 1             L 2             L 3

No processo de escalonamento preciso realiza processos de multiplicação, divisão adição e subtração para encontrar uma nova linha.

O primeiro vamos,

L 3 ' =   c 1 L 2 - b 1 L 3

Ficando,

m ' = a 1 a 2 a 3 b 1 b 2 b 3 0 c 1 b 2 - c 2 b 1 c 1 b 3 - b 1 c 3               L 1             L 2             L 3 '

L 2 ' = a 1 L 2 - b 1 L 1

m ' = a 1 a 2 a 3 0 a 1 b 2 - b 1 a 2 a 1 b 3 - b 1 a 3 0 c 1 b 2 - c 2 b 1 c 1 b 3 - b 1 c 3               L 1             L 2 '             L 3 '

L 2 " = b 1 L 1 + ( L 2 ' - a 1 b 2 )

m ' = a 1 a 2 a 3 - a 1 b 2 0 b 1 a 3 + a 1 b 3 - b 1 a 3 - a 1 b 2 0 c 1 b 2 - c 2 b 1 c 1 b 3 - b 1 c 3               L 1             L 2 "             L 3 '

Mudança, l2’’ para l3’

m ' = a 1 a 2 a 3 0 c 1 b 2 - c 2 b 1 c 1 b 3 - b 1 c 3 - a 1 b 2 0 b 1 a 3 + a 1 b 3 - b 1 a 3 - a 1 b 2               L 1             L 2 "             L 3 '

L 3 ' ' = l 2 ' ' * L 3 '

m ' = a 1 a 2 a 3 0 c 1 b 2 - c 2 b 1 c 1 b 3 - b 1 c 3 0 0 c 1 b 3 - b 1 c 3 ( b 1 a 3 + a 1 b 3 - b 1 a 3 - a 1 b 2 )               L 1             L 2 "             L 3 ' '

Passo 4

Quase finalizando a questão galera !!!

Vamos calcular o valor do determinante,

det ⁡ m ' = a 1 c 1 b 2 - c 2 b 1 c 1 b 3 - b 1 c 3 b 1 a 3 + a 1 b 3 - b 1 a 3 - a 1 b 2

det ⁡ m ' = ( a 1 c 1 b 2 - a 1 c 2 b 1 ) ( c 1 b 3 - b 1 c 3 ) ( b 1 a 3 + a 1 b 3 - b 1 a 3 - a 1 b 2 )

det ⁡ m ' = ( a 1 c 1 b 2 c 1 b 3 - a 1 c 1 b 2 b 1 c 3 - a 1 c 2 b 1 c 1 b 3 + a 1 c 2 b 1   b 1 c 3 ) ( b 1 a 3 + a 1 b 3 - b 1 a 3 - a 1 b 2 )

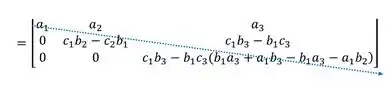
Simplificando os termos

det[ m ' ] = a 3 b 2 c 1 + c 2 b 3 a 1 + c 3 a 2 b 1 -   a 1 b 2 c 3 - c 2 b 1 a 3 - c 1 a 2 b 3

Resposta

Então, podemos concluir que a matriz

det[ m ' ] = ( - 1 ) det ⁡ m

e o i=1

Espero que ajudem nos estudos, até próxima

Exercícios de Livros Relacionados

Calcular d e t (A) nos seguintes casos:([[1,1],[2,3]]) ([[4,1],[2,0]]) ([[1,3,1],[2,1,0],[0,1,1]]) ([[1,2,1],[2,1,3],[1,0,1]]) ([[1,0,0,0],[3,2,0,0],[1,1,4,0],[4,0,1,-,1]]) ([[1,0,0,0],[0,3,0,0],[0,0,
Calcular d e t (A) nos seguintes casos:([[1,1],[2,3]]) ([[4,1],[2,0]]) ([[1,3,1],[2,1,0],[0,1,1]]) ([[1,2,1],[2,1,3],[1,0,1]]) ([[1,0,0,0],[3,2,0,0],[1,1,4,0],[4,0,1,-,1]]) ([[1,0,0,0],[0,3,0,0],[0,0,
Calcular d e t (A) nos seguintes casos:([[1,1],[2,3]]) ([[4,1],[2,0]]) ([[1,3,1],[2,1,0],[0,1,1]]) ([[1,2,1],[2,1,3],[1,0,1]]) ([[1,0,0,0],[3,2,0,0],[1,1,4,0],[4,0,1,-,1]]) ([[1,0,0,0],[0,3,0,0],[0,0,
Calcular s g n (sigma) nos seguintes casos:([[1,2,3,4],[4,3,2,1]]) ([[1,2,3,4],[2,1,4,3]]) ([[1,2,3,4,5],[2,3,4,5,1]]) ([[1,2,3,4,5,6],[4,5,6,1,2,3]])
Calcular s g n (sigma) nos seguintes casos:([[1,2,3,4],[4,3,2,1]]) ([[1,2,3,4],[2,1,4,3]]) ([[1,2,3,4,5],[2,3,4,5,1]]) ([[1,2,3,4,5,6],[4,5,6,1,2,3]])