Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 5.Problemas Propostos - Ex. 41b

Seja o paralelepípedo de dimensões 2 , 3 e 4 , representado a seguir.

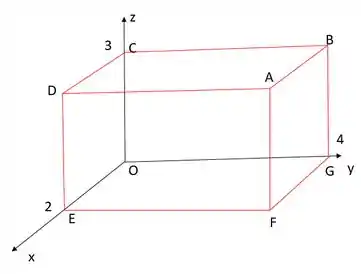
Determinar as equações da reta que contém o segmento AB

Passo 1

Para essa questão, temos que achar uma equação na forma x = x 0 + x 1 t y = y 0 + y 1 t z = z 0 + z 1 t e dela extrair a equação reduzida para termos as equações da reta que contém o segmento AB

As coordenadas ( x 1 ,   x 2 ,   x 3 ) são do vetor diretor v → da reta que passa por esses pontos e x 0 ,   y 0 ,   z 0 as coordenadas do ponto A.

Passo 2

Para acharmos as coordenadas do vetor diretor, vamos tomar como v → = A B → . Assim

Como A = 2 ,   4 ,   3 e   B = 0 ,   4 ,   3

v → = A B → = 0 ,   4 ,   3 - 2 ,   4 ,   3

v → = - 2 ,   0 ,   0

Passo 3

Analisando as coordenadas do ponto A e do vetor diretor v → , temos:

x 0 = 2 y 0 = 4 z 0 = 3 x 1 = - 2 y 1 = 0 z 1 = 0

Tomando esses pontos, a equação paramétrica da reta fica

r : x = 2 + ( - 2 ) t y = 4 + 0 t z = 3 + 0 t

r : x = 2 - 2 t y = 4 z = 3

Passo 4

Agora, com a equação paramétrica, vamos extrair a equação reduzida.

Como essa equação só possui parâmetro em x , podemos usar as equações sem parâmetros como reduzidas

r :   y = 4 z = 3

Pronto, chegamos ao fim da questão

Resposta

r : x = 2 - 2 t y = 4 z = 3 e r :   y = 4 z = 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a equação geral do plano que contém os seguintes pares de retas: r : x - 1 2 = y + 2 3 = z - 3 - 1e s : x - 1 - 2 = y + 2 - 1 = z - 3 2
Determinar as equações reduzidas, em termos de x , da reta r que passa pelo ponto A ( 2 ,- 1 ,4 ) e é perpendicular ao plano π : x - 3 y + 2 z - 1 = 0
Determinar as equações paramétricas da reta r que passa pelo ponto A ( - 1 ,0 ,0 ) e é paralela a cada um dos palnos π 1 : 2 x - y - z + 1 = 0 e π 2 : x + 3 y + z - 5 = 0
Seja o paralelepípedo de dimensões 2 , 3 e 4 , representado a seguir. Determinar a equação do plano que contém a face ABGF
Seja o paralelepípedo de dimensões 2 , 3 e 4 , representado a seguir. Determinar as equações da reta que contém o segmento EF