Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 23.Problemas - Ex. 5

Seja T   :   R ² →   R ² a transformação linear que consiste em aplicar uma rotação de ângulo θ e depois trocar o sinal da segunda coordenada. Mostre que T é a reflexão em torno de uma reta r que contém a origem e é tal que o ângulo de OX para r é - θ / 2 .

Passo 1

Saudações galerinha, tudo bem?

Vamos começar a resolver mais um exercício, bora lá então!

Inicialmente começaremos alertando que esse exercício pode ser feito de várias formas diferentes, beleza!

Considere o que acontece quando tomamos um ponto ( x   ,   y ) e gire-o em um ângulo de θ

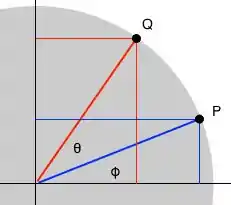
Usando coordenadas polares, podemos escrever (   x   ,   y )   =   (   r c o s   ϕ   ,   r   s e n ϕ )Onde r é a distância de (   x   ,   y ) para a origem e   ϕ é o ângulo formado pela reta desde a origem até (   x   ,   y ) e o positivo x-eixo.

Depois de rodar (   x   ,   y ) por um ângulo de θ , o novo ponto ainda é r unidades de distância da origem, mas agora, o ângulo feito pela linha da origem para ( x ' , y ' ) e o positivo x-eixo aumenta em θ . Por isso , ( x ' , y ' )   =   (   r c o s   (   ϕ   +   θ   )   ,   r   s e n (   ϕ   +   θ   )   ) .

Agora, vamos usar a soma do cosseno e do seno das fórmulas de ângulo para escrever x ' e y '   em termos de x   e y :

x ' =   r   c o s (   ϕ   +   θ   )   =   r   c o s ϕ   c o s θ   -   r   s e n ϕ   s e n θ   =   x   c o s θ   –   y s e n θ

y ' =   r   s e n (   ϕ   +   θ   )   =   r   s e n ϕ   c o s θ   +   r   c o s ϕ   s e n θ   =   y s e n θ   +   x   s e n θ

Passo 2

Continuando!

Colocando isso em forma de matriz nos vamos obter

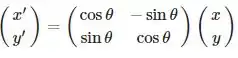
Portanto, a matriz que gira um ponto em um ângulo de θ anti-horário é:

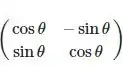
Prontinho!

Te vejo na próxima questão.

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Admitindo que a1 e a2 não são simultaneamente nulos, prove que a 1 b 2 - a 2 b 1 = 0 e a 1 c 2-a 2 c 1=0 implicam b 1 c 2-b 2 c 1 =0 .
Dadas as matrizes m = a 1 b 1 a 2 b 2 e n = c 1 d 1 c 2 d 2 Defina as funções M , N : R 2 →R 2 (transformações lineares) pondo, para cada x , y ∈ R 2 ,M x , y = a 1 x + b 1 y , a 2 x + b 2 y ) ,N ( x
Seja m uma matriz 3x3o u3x4 . Diz-se que m tem 1 quando uma de suas linhas é não-nula e as outras são múltiplos dela. Prove que, neste caso, uma de suas colunas ´e não-nula e as outras colunas são múl
Enuncie e demonstre o análogo para R 3 do exercício 3 da Seção 35. Conclua que todas as propriedades do determinante são consequências destas quatro.
Uma matriz quadrada m chama-se quando m t = m - 1 . Prove que m é ortogonal se, e somente se, seus vetores-linha (ou coluna) são dois a dois ortogonais de comprimento 1. Dê exemplos de matrizes ortogo