Sejam B= ( a → , b → , c → ) uma base de V , u →=( x , y , z ) B . Que condições devem satisfazer x , y e z para que ( a →+u → , b →+u → , c →+u → ) sejam também uma base de V ?

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 2.Exercícios Propostos - Ex. 30

Sejam uma base de , . Que condições devem satisfazer , e para que sejam também uma base de ?

Passo 1

Pessoal, antes de mais nada temos que relembrar o que define uma base. De acordo com o livro, uma base é uma sequência de três vetores L.I. Então, se é uma base de , quer dizer que são L.I. Outra coisa que temos que entender é o que significa a notação . Isso nada mais é que uma forma de escrever que

Sabendo disso, podemos notar que

Então, o segundo conjunto de vetores será escrito como

Nesse caso, é melhor escrever esses vetores na mesma notação que . Assim,

Passo 2

A condição para que o conjunto de vetores obtidos no passo anterior seja uma base é que todos os vetores sejam L.I. Para mostrar que isso é verdade, o determinante da matriz formada pelos três vetores tem que ser diferente de zero. Vamos montar essa matriz, calcular seu determinante e ver qual a condição para que o determinante não seja nulo:

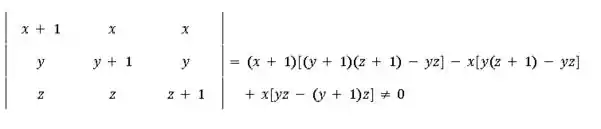
Então, a condição para que sejam também uma base de é que .

Resposta

Exercícios de Livros Relacionados

Considerando a Figura 3.13, calcularf) vec G B xx vec A F

Considerando a Figura 3.13, calculare) vec O A . ( vec O C xx vec O E )

Sejam os vetores vec u = (1 , - 2 , 1) , vec v = ( 1 , 1 , 1 ) e vec w = ( 1 , 0 , - 1 ) .c) Mostre que vec u xx (vec v xx vec w) = vec 0 .

Obter um vetor ortogonal ao plano determinado pelos pontos A ( 2 ,3 ,1 ) , B ( 1 ,- 1 ,1 ) e C ( 4 ,1 ,- 2 ) .

Determinar um vetor simultaneamente ortogonal aos vetores u → + 2 v → e v → - u → , sendo u → = ( - 3 ,2 ,0 ) e v → = ( 0 ,- 1 ,- 2 ) .