Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 3.Problemas propostos - Ex. 7e

Considerando a Figura 3.13, calcular

e) vec O A . ( vec O C xx vec O E )

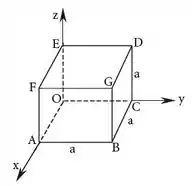
Passo 1

Pra começar, vamos observar que na figura do exercício a gente tem um cubo de lado a certo? Então, antes de qualquer coisa, vamos dar as coordenadas de todos os pontos que temos, com base na sua localização nos eixos x , y , z .

A = ( a , 0 , 0 )

B = ( a , a , 0 )

C = ( 0 , a , 0 )

D = ( 0 , a , a )

E = ( 0 , 0 , a )

F = ( a , 0 , a )

G = ( a , a , a )

O = ( 0 , 0 , 0 )

Agora sim, vamos fazer o produto pedido pelo enunciado :)

Passo 2

Queremos calcular vec O A . ( vec O C xx vec O E ) , ou seja, primeiro vamos calcular o produto vetorial entre o vetor vec O C e vec O E , dentro dos parênteses, e aí depois fazemos o produto escalar desse resultado com o vetor vec O A .

Primeiro vamos encontrar nossos vetores:

vec O C = C - O = ( 0 , a , 0 )

vec O E = E - O = ( 0 , 0 , a )

vec O A = A - O = ( a , 0 , 0 )

Agora podemos calcular o produto vetorial vec O C xx vec O E = ( 0 , a , 0 ) xx ( 0 , 0 , a ) , ele é dado pelo determinante:

|[[vec i,vec j,vec k],[0,a,0],[0,0,a]]|

Calculando esse determinante, temos

|[[vec i,vec j,vec k],[0,a,0],[0,0,a]]| = a ² . vec i + 0 . vec j + 0 . vec k

Logo, temos que vec O C xx vec O E = ( a ² , 0 , 0 ) .

Passo 3

Agora que fizemos o produto vetorial que tínhamos dentro do parênteses, vamos calcular o produto escalar

vec O A . ( vec O C xx vec O E )

Lembrando que vec O A = ( a , 0 , 0 ) e vec O C xx vec O E = ( a^2 , 0 , 0 ) - calculamos no passo anterior -, temos:

(a , 0 , 0) . ( a^2 , 0 , 0 )

Fazendo o produto escalar:

a . a^2 + 0.0 + 0.0

a ³

Resposta

a ³

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dados os vetores a → = ( 3 ,4 ,2 ) e b → = ( 2 ,1 ,1 ) , obter um vetor de módulo 3 que seja ao mesmo tempo ortogonal aos vetores 2 a → - b → e a → + b → .
Mostrar que o quadrilátero cujos vértices são os pontos A 1 ,- 2 ,3 , B 4 ,3 ,- 1 , C ( 5 ,7 ,- 3 ) e D ( 2 ,2 ,1 ) é um paralelogramo e calcular sua área.
Dados os vetores u → = 2 ,1 ,0 e v → = ( 3 , - 6 ,9 ) , determinar o vetor x → que satisfaz a relação v → = u → × x → e que seja ortogonal ao vetor w → = ( 1 , - 2 ,3 ) .
Dado o triângulo de vértices A 0 ,1 , - 1 , B ( - 2 ,0 ,1 ) e C ( 1 , - 2 ,0 ) , calcular a medida da altura relativa ao lado B C .
Sejam u , v e w vetores não nulos com o mesmo ponto inicial no espaço tridimensional, mas tais que dois quaisquer não são colineares. Mostre que u × v × w está no plano determinado por u e v