Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 3.Exercícios Propostos - Ex. 21

Os vetores x → e y → formam um ângulo de 60 ° . Sabendo que x → = 1 , y → = 2 , a → = x → + 2 y → e b → = 2 x → - y → , pedem-se: | a → | , b → e o ângulo entre a → e b → . Num desenho, represente x → , y → , a → , b → e o ângulo achado.

Passo 1

Falaa galeraa, beleza??

Para encontrar o que a questão pede vamos primeiro achar o produto escalar entre x → e y → a partir do valor do cosseno de 60 ° :

c o s 60 ° = x → ⋅ y → x → ⋅ y →  

1 2 = x → ⋅ y → 1 ⋅ 2

x → ⋅ y → = 1

Passo 2

Agora vamos achar a → ⋅ b → :

a → ⋅ b → = x → + 2 y → ⋅ ( 2 x → - y →   )

a → ⋅ b → = 2 x → ⋅ 2 x → - x → ⋅ y → + 4 x → ⋅ y → - 2 y → ⋅ y →

a → ⋅ b → = - 3

Passo 3

Show! Agora, vamos usar a lei dos cossenos para calcular os módulos de a → e de b → :

a → 2 = x → 2 + 2 y → 2 - 2 x → 2 y → c o s 60 °

a → 2 = 1 2 + 4 2 - 2 ⋅ 1 ⋅ 2 ⋅ 2 ⋅ - 1 2

| a → | = 21

b → 2 = 2 x → 2 + y → 2 - 2 2 x → y → c o s 60 °

b → 2 = 2 2 + 2 2 - 2 ⋅ 2 ⋅ 1 ⋅ 2 ⋅ 1 2

b → = 2

Por fim, vamos calcular o cosseno do ângulo entre eles:

c o s α = - 3 21 ⋅ 2 = - 21 14

Passo 4

Agora, faltam só os desenhos dos vetores:

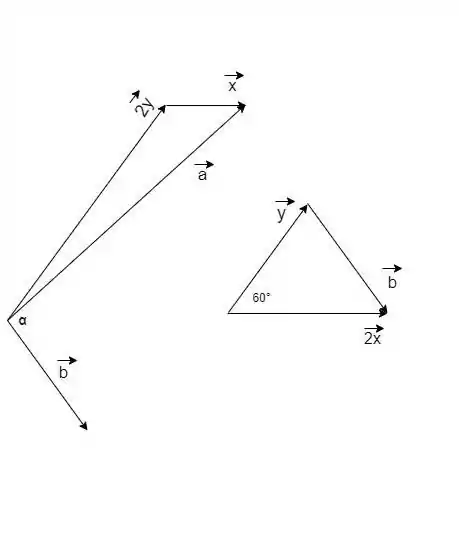
Fechou! Vamos pra próxima??

Resposta

| a → | = 21

b → = 2

c o s α = - 21 14

Exercícios de Livros Relacionados

Prove que são verdadeiras as afirmações seguintes.(a) A B → . C D → + B C → . A D → + C A → . B D → = 0 , quaisquer que sejam os pontos A, B, C e D (Relação de Euler).
Sejam a → e b → nao-nulos.(c) Por analogia, tente generalizar os resultados dos itens (a) e (b) para n projeções sucessivas .
As retas que contêm alturas de um triângulo são concorrentes num ponto, chamado ortocentro do triângulo. (Este resultado foi objeto do Exercício 5-21. Sua verificação, com o auxílio da Relação de Eule
Sejam vec a e vec b nao-nulos.(a) Prove que p r o j_vec v p r o j_vec u vec v = ((vec u . vec v)^2)/(|vec u|^2 |vec v|^2) vec v .
Sejam a → e b → nao-nulos.(b) Enuncie uma condição necessária e suficiente para que a projeção ortogonal de a → sobre b → e a de b → sobre a → tenham normas iguais.