Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 45
Prove que as bissetrizes de ângulos adjacentes suplementares são perpendiculares.
Passo 1
Vamos lembrar primeiro o que são ângulos suplementares:
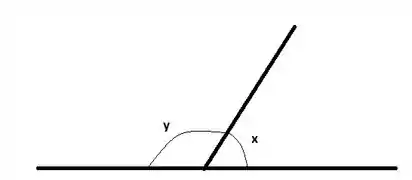
Eles somados formam :
Passo 2
Traçando as bissetrizes em cada ângulo:
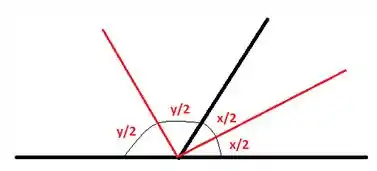
O ângulo entre as bissetrizes é
Passo 3
Assim,
Mas sabemos que . Logo,
Portanto, o ângulo entre as bissetrizes é reto: elas são perpendiculares!
Resposta
Demonstração.
Exercícios de Livros Relacionados
São dadas as coordenadas de u → e v → em relação a uma base ortonormal fixada. Calcule, em radianos, a medida angular entre u → e v → . u → = 3 ,3 ,0 e v → = ( 2 ,1 ,- 2 )
Verdadeiro ou falso?a) A medida angular entre um vetor não-nulo e ele mesmo é 0 (graus ou radianos).b) A medida angular entre dois vetores não-nulos e ortogonais é π / 2 radianos. c) A medida angular
Em uma roleta de centro O , o preto 17 ocupa a posição P . Após um giro de 7 π / 5 rad, passa a ocupar a posição Q . Qual é a medida angular em radianos entre O P → e O Q → ?
São dados os números reais positivos a e b , e o vetor u → , de norma a . Dentre os vetores de norma b , qual é o que torna o produto escalar u → ⋅ v → máximo? E mínimo? Quais são esses valores máximo
Os lados do triângulo equilátero A B C têm medida 2. Calcule A B → ⋅ B C → + B C → ⋅ C A → + C A → ⋅ A B → .