Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 6.Exercícios Propostos - Ex. 14

Sejam A = 1,0 , 1 , B = 0,1 , 1 , C = ( 3 , - 2,1 ) e D = ( 0,0 , 1 ) . (a) Determine um ponto X na reta A B tal que a área do triângulo C D X seja 2. Quantos pontos X existem nessas condições?

(b) Qual a distância de X à reta C D ? (c) Represente num desenho plausível os pontos A , B , C , D e X .

Passo 1

Fala ae, galera! Tudo bem? 😊

Letra (a):

Precisamos descobrir quem é a reta A B , para isso queremos achar seu vetor diretor e um ponto que pertence a essa reta.

O vetor diretor de A B é:

A B → = B - A = ( - 1,1 , 0 )

Como A = ( 1,0 , 1 ) pertence a reta A B , sua equação da reta é:

A B : x = 1 - t y = t z = 1 ; t   ∈ R

Passo 2

Como o ponto X pertence a reta A B , ele é um ponto que satisfaz as coordenadas da reta, assim:

X = ( 1 - t , t , 1 )

A área do triângulo C D X é dada por:

S C D X = 1 2 d e t ⁡ C D → C X → = 2   ( i )

Vamos identificar os vetores:

C D → = D - C = - 3,2 , 0

C X → = X - C = 1 - t - 3 , t + 2,0 = ( - 2 - t , t + 2,0 )

Passo 3

Agora, vamos fazer o determinante desses vetores:

d e t ⁡ C D → C X → = d e t - 3 2 0 - 2 - t t + 2 0 1 1 1 = - 3 t + 2 - 2 - 2 - t

d e t ⁡ C D → C X → = - 3 t - 6 + 4 + 2 t = - t - 2

Substituindo em i :

4 = - t - 2

t = - 6

Ou:

- 4 = - t - 2

t = 2

Assim,

X = 7 , - 6,1   o u   X = ( - 1,2 , 1 )  

Passo 4

Letra (b):

Para descobrirmos quem é a reta C D , devemos achar seu vetor diretor e um ponto que pertence a essa reta.

O vetor diretor de C D é:

C D → = D - C = ( - 3,2 , 0 )

Como D = ( 0,0 , 1 ) pertence a reta C D , sua equação da reta é:

C D : x = - 3 s y = 2 s z = 1

A distância de C D para X é dada por:

d C D , X = 2 7 + 3 - 6 2 2 + 3 2 = 4 13

Ou:

d C D , X = 2 - 1 + 3 2 2 2 + 3 2 = 4 13

Passo 5

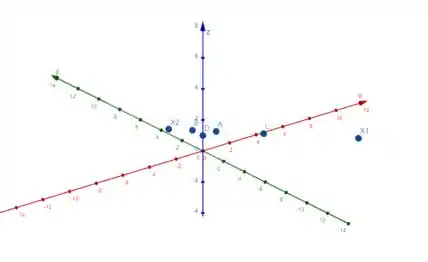
Letra (c):

Posicionando os pontos A , B , C ,   D   e   X no espaço, temos o seguinte esboço:

Resposta

L e t r a a :   X = 7 , - 6,1   o u   X = ( - 1,2 , 1 )  

L e t r a b : d C D , X = 4 13

L e t r a   c :  

Exercícios de Livros Relacionados

Sejam A = 0 ,2 ,1 e r : X = 0 ,2 ,- 2 + λ ( 1 ,- 1 ,2 ) . Obtenha os pontos de r que distam 3 de A . Em seguida verifique se a distância do ponto A à reta r é maior, menor ou igual a 3 e justifique su
Sejam P = ( 2 ,1 ,- 1 ) e Q = ( 0 ,- 1 ,0 ) . Determine um ponto C da reta P Q tal que a área do triângulo A B C seja 9 , nos casos:b) A = - 2 ,3 ,4 ,B = ( - 6 ,- 1 ,6 )
Sejam P = ( 2 ,1 ,- 1 ) e Q = ( 0 ,- 1 ,0 ) . Determine um ponto C da reta P Q tal que a área do triângulo A B C seja 9 , nos casos:d) A = 1 ,2 ,7 ,B = ( - 5 ,- 4 ,- 5 )
Sejam P = ( 2 ,1 ,- 1 ) e Q = ( 0 ,- 1 ,0 ) . Determine um ponto C da reta P Q tal que a área do triângulo A B C seja 9 , nos casos:c) A = - 1 ,1 ,2 ,B = ( - 5 ,- 3 ,4 )
Sejam P = ( 2 ,1 ,- 1 ) e Q = ( 0 ,- 1 ,0 ) . Determine um ponto C da reta P Q tal que a área do triângulo A B C seja 9 , nos casos:a) A = 0 ,3 ,0 ,B = ( 6 ,3 ,3 )