Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 5.2 - Ex. 17a

Sejam W_1 e W_2 dois subespaços.

a) Mostre que W_1 nn_()^() W_2 .

Passo 1

Eaew, tudo em cima?

Vamos lembrar a definição de um subespaço, beleza? Se nós temos uma matriz m xx n e W sub R^m o conjunto solução do sistema linear homogêneo A X = overset(̄)(0) , em que W respeita as seguintes propriedades:

a) Se X e Y pertencem a W , então X + Y também pertence a W .

b) Se X pertence a W , então alpha X também pertence a W para todo escalar alpha .

Se temos um subconjunto não vazio que obedece a) e b), então ele é um subespaço do R^m . Belezinha? Isso já é o suficiente para demonstrarmos o que precisamos, bora lá!

Passo 2

Note que para ser um subespaço de R^m temos que W_1 e W_2 devem estar individualmente contidos em R^m . Vamos analisar esta alternativas em termos de diagramas de Venn, temos o seguinte conjunto:

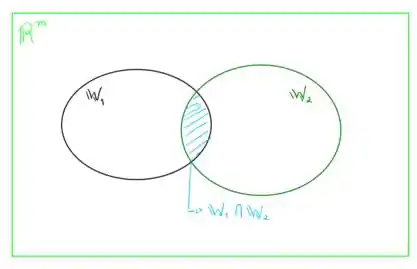
Note que como a intersecção está contida tanto em W_1 quanto em W_2 , ela necessariamente tem as mesmas propriedades de ambos e também está contida em R^m , ou seja, é um subespaço! Vamos para a próxima alternativa!

Resposta

Demonstrado pelo diagrama de Venn

Exercícios de Livros Relacionados

Encontre os valores de λ tais que o sistema homogêneo (A - λ I n )X = 0 tem solução não trivial e para estes valores de λ, encontre uma base para o espaço solução, para as matrizes A dadas:e) A =2 3 0
Encontre os valores de λ tais que o sistema homogêneo (A - λ I n )X = 0 tem solução não trivial e para estes valores de λ, encontre uma base para o espaço solução, para as matrizes A dadas:e) A =2 3 0
Encontre os valores de λ tais que o sistema homogêneo (A - λ I n )X = 0 tem solução não trivial e para estes valores de λ, encontre uma base para o espaço solução, para as matrizes A dadas: d )A =- 1
Encontre os valores de λ tais que o sistema homogêneo (A - λ I n )X = 0 tem solução não trivial e para estes valores de λ, encontre uma base para o espaço solução, para as matrizes A dadas: A =0 0 1 1
Encontre os valores de λ tais que o sistema homogêneo (A - λ I n )X = 0 tem solução não trivial e para estes valores de λ, encontre uma base para o espaço solução, para as matrizes A dadas:b) A =2 2 3