Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 5.2 - Ex. 7
Considere os seguintes subespaços de
e
Encontre as equações paramétricas da reta e uma base para o subespaço . A notação significa o subespaço gerado por e , ou seja, o conjunto de todas as combinações lineares de e .
Passo 1
Oiie, tudo certinho? Vamos começar?
Para formar a base desejada é interessante lembrar que a intersecção entre ambos os planos (note que é um subespaço tridimensional, mas que é formado por dois vetores, portanto planos) é dada por uma reta cujo vetor diretor é dado por:
em que e são os vetores normais dos dois planos. Vamos então achar isso primeiro, beleza?
Passo 2
Podemos achar o vetor normal como:
obtido fazendo o determinante da seguinte matriz:
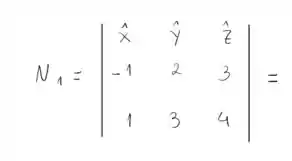
Portanto, temos:
Analogamente para , temos:
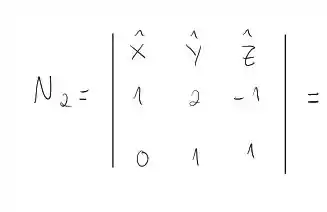
ou seja:
Vamos agora achar a intersecção reta deste dois planos e checar se o vetor é nulo ou não. Porque isso irá nos dizer a base! Belezinha?
Passo 3
Temos que a reta interseção é dada como:
em que é um parâmetro qualquer da reta e é o vetor diretor dessa reta, bora lá então!
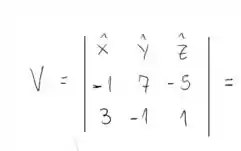
tal que:
De forma que a reta interseção é da seguinte forma:
E como ela é não nula, temos que esta é a base da reta, como pedido no enunciado. A questão foi isso, te vejo na próxima!