Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios de Base - Lista de Exercícios Resolvida

Ver Teoria

Questão 1

Sejam u 1 → ,   … ,   u n → vetores gerando um espaço vetorial V .

Sejam v 1 → ,   … ,   v k → ∈ V , vetores linearmente independentes.

Assinale a alternativa VERDADEIRA:

a   n ≥ k

b   n = k

c   n ≤ k

d   n > k

Ver solução completa

Questão 2

Seja V um espaço vetorial e S = { v 1 → ,   v 2 → ,   v 3 → ,   v 4 → } um conjunto de vetores de V , todos distintos entre si.

Sejam A = { v 1 → ,   v 2 → } e B = { v 3 → ,   v 4 → } .

Assinale a alternativa VERDADEIRA:

( a ) Se S é um conjunto linearmente independente ( L I ), então A é um conjunto linearmente independente ( L I ) e B é um conjunto linearmente independente ( L I ).

( b ) Se S é um conjunto gerador de V , então A é um conjunto gerador de V e B é um conjunto gerador de V

( c ) Se S é um conjunto linearmente independente (LI), ou A é um conjunto linearmente independente (LI), ou B é um conjunto linearmente independente (LI), mas não ambos.

( d ) Se S é um conjunto gerador de V , então: ou A é um conjunto gerador de V , ou B é um conjunto gerador de V , mas não ambos.

Ver solução completa

Questão 3

Seja H o subespaço definido por:

H =   < 2 , - 1 ,   - 1 ,   2 ,   - 2 ,   1 ,   - 4 ,   1 ,   4 ,   0 ,   2 ,   - 4 >

Qual dos conjuntos abaixo é base de H ?

a   { 2 , - 1 ,   - 1 }

b   { 2 , - 1 ,   - 1 ,   2 ,   - 2 ,   1 ,   - 4 ,   1 ,   4 ,   0 ,   2 ,   - 4 }

c   { 2 , - 1 ,   - 1 ,   2 ,   - 2 ,   1 }

d   2 , - 1 ,   - 1 ,   2 ,   - 2 ,   1 ,   - 4 ,   1 ,   4

Ver solução completa

Questão 4

Seja o subespaço S de M 2 × 2 :

S = a b c d c = a + b   e   d = a }

O conjunto

1 - 1 0 1 ,   2 1 3 4

É uma base de S ?

Ver solução completa

Questão 5

Quais dos seguintes conjuntos de polinômios formam base de P 2 ?

  1. 2 t 2 + t - 4 ,   t 2 - 3 t + 1
  2. 1 ,   t ,   t 2
  3. 2 ,   1 - x ,   1 + x 2
  4. 1 + x + x 2 ,   x + x 2 ,   x 2
  5. { 1 + x ,   x - x 2 ,   1 + 2 x - x 2 }  

Ver solução completa

Questão 6

Mostrar que o conjunto

2 3 - 1 0 ,   1 - 1 0 - 2 ,   - 3 - 2 1 - 1 ,   3 - 7 - 2 5

É uma base de M 2 × 2 .

Ver solução completa

Questão 7

Sejam V = M 2 ( R ) ,

S = A ∈ V   |     A 1 0 0 2 = 1 0 0 2 A e   T = a b c d ∈ V   |   b + c = 0    

Nestas condições podemos afirmar:

Ver solução completa

Questão 8

Dadas as matrizes

A =   1 0 0 0 ,         B = 1 2 0 1 ,         C = 0 0 1 0 ,         D = 0 2 1 1

Considere as seguintes afirmações:

I   S ã o   l i n e a r m e n t e   i n d e p e n d e n t e s ;  

I I   G e r a m   u m   s u b e s p a ç o   d e   M 2 R   d e   d i m e n s ã o   3 ;

I I I   F o r m a m   u m a   b a s e   d e   M 2 R .

Ver solução completa

Questão 9

Seja V um espaço vetorial de dimensão n ≥ 1 ,   e seja B = v 1 , … ,   v k   um subconjunto de V contendo k vetores distintos. Considere as seguintes afirmações:

I .   Se V = B ,   então, necessariamente, k = n

I I . Se B é linearmente independente e k = n , então B é base de V

I I I . Se v 1 , … , v k - 1 é base de um subespaço vetorial W   d e   V e v k ∉ W , então B é linearmente independente.

Está correto apenas o que se afirma em

a )   I   e   I I

b )   I

c )   I   e   I I I

d )   I I

e )   I I   e   I I I

Ver solução completa

Questão 10

Seja { u 1 , u 2 , u 3 } uma base de R 3 , munido do produto interno usual, e seja { v 1 , v 2 , v 3 } a base obtida de { u 1 , u 2 , u 3 } por meio do processo de ortogonalização de Gram-Schmidt. Se u 3 = 0,2 , - 1   e   v 3 = ( - 1,1 , 0 ) então p r o j [ v 1 , v 2 ] u 3 é igual a

a   - 1 , - 1,1

b   1 , - 1,1

c   - 1,3 , - 1

d   1,1 , - 1

e   ( 1 , - 1 , - 1 )

Ver solução completa

Questão 11

Seja W = a , b , c , d , e , f a = 0 , c = d + 3 b , d = 2 b - f , b = 2 f um subespaço de R 6 . A dimensão de W é igual a:

( a ) 4

( b ) 3

( c ) 1

( d ) 2

Ver solução completa

Questão 12

Seja H o subespaço definido por:

H =   2 , - 1 ,   - 1 ,   2 ,   - 2 ,   1 ,   - 4 ,   1 ,   4 ,   0 ,   2 ,   - 4

Qual dos conjuntos abaixo é base de H ?

( a ) 2 , - 1 ,   - 1

( b ) 2 , - 1 ,   - 1 ,   2 ,   - 2 ,   1 ,   - 4 ,   1 ,   4 ,   0 ,   2 ,   - 4

( c ) 2 , - 1 ,   - 1 ,   2 ,   - 2 ,   1

( d ) 2 , - 1 ,   - 1 ,   2 ,   - 2 ,   1 ,   - 4 ,   1 ,   4

Ver solução completa

Questão 13

Seja V um espaço vetorial e S = { v 1 → ,   v 2 → ,   v 3 → ,   v 4 → } um conjunto de vetores de V , todos distintos entre si.

Sejam A = { v 1 → ,   v 2 → } e B = { v 3 → ,   v 4 → } .

Assinale a alternativa VERDADEIRA:

( a ) Se S é um conjunto linearmente independente ( L I ), então A é um conjunto linearmente independente ( L I ) e B é um conjunto linearmente independente ( L I )

( b ) Se S é um conjunto gerador de V , então A é um conjunto gerador de V e B é um conjunto gerador de V

( c ) Se S é um conjunto linearmente independente ( L I ), ou A é um conjunto linearmente independente ( L I ), ou B é um conjunto linearmente independente ( L I ), mas não ambos.

( d ) Se S é um conjunto gerador de V , então: ou A é um conjunto gerador de V , ou B é um conjunto gerador de V , mas não ambos.

Ver solução completa

Questão 14

Considere as afirmações abaixo:

(I) 1,2 , 3 , 0,4 , 5 , 0,0 , 6 é gerador de R 3 .

(II) { 1,1 , 1 , 1,2 , 3 , 1,1 , 4 } é uma base de R 3 .

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Ver solução completa

Questão 15

Seja V um espaço vetorial munido de um produto interno . , .   e considere as seguintes afirmações:

I )   Se e 1 , e 2 , … ,   e n é uma base de V e se v ∈ V é tal que v , e i = 0 , para i = 1,2 , . . , n , então v = 0

I I ) Se S é um subespaço de V e se e 1 , e 2 , … ,   e m   ∈ S são vetores dois a dois distintos tais que e 1 , e 2 , … ,   e n é uma base de S, então

p r o j S   v = p r o j e 1 v + p r o j e 2 v + … + p r o j e n v

Para qualquer v ∈ V

I I I )   Se v , w   ∈ V , λ ∈ R , v ≠ 0 e λ ≠ 0 , então:

p r o j λ v   w = λ   p r o j v   w

Assinale a alternativa correta:

a )   Apenas as afirmações I   e   ( I I I ) são necessariamente verdadeiras

b )   Apenas as afirmações I   e   ( I I ) são necessariamente verdadeiras

c )   Apenas as afirmações I I   e   ( I I I ) são necessariamente verdadeiras

d ) Apenas a afirmação ( I ) é necessariamente verdadeira

e ) Todas as afirmações são necessariamente verdadeiras;

Ver solução completa

Questão 16

Seja β uma base de V 3 . Forma com os vetores 1 , - 3,2 β e 2,3 , - 1 β um conjunto linearmente dependente o vetor

a) - 5,5 , - 6

b) 3,9 , - 4

c) - 7,4 , - 5

d) 8 , - 3 , - 1

e) 5 , - 5,4

Ver solução completa

Questão 17

b Encontre uma base para W = a 0 + a 1 x + a 2 x 2 ∈ P 2 R ; a 0 - 2 a 1 + a 2 = 0 .

Ver solução completa

Questão 18

Seja V = R 3 , e seja W o conjunto solução do sistema linear homogêneo cuja matriz de coeficientes é

A = 1 2 3 4 5 6 7 8 9

a Justifique porque W é subespaço de V , e ache uma base para W .

b Estenda a base obtida acima (item a ) para obter uma base de V .

Ver solução completa

Questão 19

Seja β uma base ortonormal de V 3 . Considere, em E 3 , o triângulo de vértices A ,   B ,   C , em que A B → = 3 , - 2,2 β e B C → = 0,1 , 1 β . A altura desse triângulo relativa ao vértice C é igual a

Ver solução completa

Questão 20

Assinale o polinômio que não pertence ao espaço W = x 3 + x 2 + 2 x + 6,2 x 2 + 2 x + 6,2 x 2 + 3 x + 9

( a ) x 3 - x 2

( b ) x + 3

( c ) x + 6

( d ) 3 x 2 + 4 x + 12

Ver solução completa

Questão 21

Considere os vetores v → = 1,1 , 0 ,   w → = ( - 1,1 , 0 ) , o plano

π : X = 1,1 , 0 + λ v → + μ w → ,     λ ,   μ   ∈ R

E a base B = v → , w → , v → ∧ w → de V 3 . Uma equação geral para o plano π no sistema de coordenadas ( O , B ) é:

a )   z = 0 ;

b )   x + y + z = 0 ;

c )   x - y - z + 2 = 0 ;

d )   x + y = 0 ;

e )   x + y + z - 1 = 0 .

Ver solução completa

Questão 22

Assinale o vetor que adicionado ao conjunto { ( 1,2 , 3 ) , ( 2,4 , 9 ) } forma uma base para o R 3 :

(a) ( 0 ,   0 ,   6 )

(b) ( 3 ,   6 ,   12 )

(c) ( 6 ,   - 3 ,   0 )

(d) ( 1 ,   2 ,   6 )

Ver solução completa

Questão 23

Seja v 1 → , v 2 → , v 3 →   uma base de G e w →   um vetor não-nulo de G . Verifique as afirmativas abaixo:

I - w → necessariamente pertence a um dos planos v 1 → , v 2 → , v 1 → , v 3 → ou v 2 → , v 3 →

II - Se w → , v 1 → , v 2 → e w → , v 1 → , v 3 → são L D , então w → , v 2 → , v 3 →   é L I

(a) I é verdadeira e II é falsa

(b) I é verdadeira e II é verdadeira

(c) I é falsa e II é verdadeira

(d) I é falsa e II é falsa

Ver solução completa

Questão 24

Considere os planos π e ρ de equações cartesianas

π : x - y - z = 0

ρ : 2 x + y + z = 0

(a) Determine uma base β de π e uma base γ de ρ tais que as duas bases tenham um vetor comum.

Ver solução completa

Questão 25

Seja   v 1 → ,   v 2 → ,   v 3 →   uma base de G e {   w 1 → ,   w 2 → ,   w 3 → }   ⊂   G , um subconjunto   L I de G . Verifique as afirmativas abaixo:

I -   w 1 → ,   v 1 → ,   v 2 → , {   w 1 → ,   v 1 → ,   v 3 → } e   w 1 → ,   v 2 → ,   v 3 →   podem ser todos, simultaneamente, conjuntos L D

II -   w 1 → ,   v 1 → ,   v 2 → , {   w 1 → ,   v 1 → ,   v 3 → } e   w 1 → ,   v 2 → ,   v 3 → podem ser todos, simultaneamente, conjuntos L I

III - Se o conjunto   w 1 → ,   v 1 → ,   v 2 →   é LI, então ele também é um conjunto gerador de G

(a) Todas são falsas

(b) II é falsa e I e III são verdadeiras

(c) I é verdadeira e II e III são falsas

(d) I é falsa e II e III são verdadeiras

(e) III é verdadeira e I e II são falsas

(f) II é verdadeira e I e III são falsas

(g) III é falsa e I e II são verdadeira

Ver solução completa

Questão 26

Encontre uma base para W = a b c d ∈ M 2 × 2 R ; a + 2 b - c = 0   e   a + b + c - 2 d = 0

Ver solução completa

Questão 27

Que condições a e b devem satisfazer a fim de que v   =   ( 1 ,   2 ,   3 ,   b ) seja combinação linear de v 1 = ( 1 ,   2 ,   1 ,   0 ) , v 2 = - 1 ,   - 1 ,   0 ,   0 ,     v 3 = ( 2 ,   1 ,   - 1 ,   a ) e v 4   =   ( 0 ,   4 ,   2 ,   2 ) ?

Ver solução completa

Questão 28

Seja E uma base de V 3 . Assinale a alternativa correspondente ao vetor v   ∈   V que torna o conjunto

{ v , ( 1 ,   − 1 ,   1 ) e   , ( 2 ,   1 ,   3 ) e   }

linearmente independente.

  1. v   =   ( 3 ,   1 ,   4 )
  2. v   =   ( − 1 , �� 4 ,   0 )
  3. v   =   ( − 1 ,   4 ,   0 )
  4. v   =   ( − 1 ,   7 ,   1 )
  5. v   =   ( 2 ,   − 2 ,   2 )

Ver solução completa

Questão 29

{ a , b , c , 1,0 , 1 , 0,1 , 1 } é base do R 3 se:

(a) a - b + c ≠ 0

(b) a + b - c ≠ 0

(c) a - b - c ≠ 0

(d) a - b - c = 0

Ver solução completa

Questão 30

Sejam { v 1 → ,   v 2 → ,   v 3 → } uma base de G e w →   ∈ G .

(I) O vetor w →   necessariamente pertence a um dos planos < v 1 → ,   v 2 → > ,   < v 2 → ,   v 3 → > ou < v 1 → ,   v 3 → > .

(II) Se { w → ,   v 1 → ,   v 2 → } e { w → ,   v 1 → ,   v 3 → } são LI, então { w → ,   v 2 → ,   v 3 → } é LD.

(a) I é verdadeira e II é verdadeira.

(b) I é falsa e II é falsa.

(c) I é verdadeira e II é falsa.

(d) I é falsa e II é verdadeira.

Ver solução completa

Questão 31

Considere o espaço vetorial M 2 × 2 das matrizes de duas linhas e duas colunas e dois subconjuntos:

U = A ∈ M 2 × 2   D e t A = 0 }

V = a c b d ∈   M 2 × 2   a + c = 0   e   b + d = 0 }

(c) Determine uma base de V.

Ver solução completa

Questão 32

Considere a base

E seja R

Se   α ,   β ,   γ ,   δ   ∈   R são tais que   R   =   ( α ,   β ,   γ ,   δ ) B , então   α   +   β   +   γ   +   δ é igual a:

  1. 7
  2. 0
  3. - 11
  4. 4
  5. 2

Ver solução completa

Questão 33

Considere u → = 1,0 , 1 B , v → = 1,1 , 0 B , w → = 2 , - 1,1 B , onde B é a base ortonormal de V 3 . Suponha que w → = x → + y → , onde x → é uma combinação linear de u →   e   v →   e   y → é ortogonal tanto a u → como a v → . Se

y → = a , b , c B

Então a + b + c   é   i g u a l   a :

a ) - 4 3

b ) 10 3

c ) 8 3

d ) - 2 3

e ) 4 3

Ver solução completa

Questão 34

Considere o espaço vetorial R 4 munido do seu produto interno usual e seja B = v 1 , v 2 , v 3 , v 4 uma base de R 4 . Suponha que C = w 1 , w 2 , w 3 , w 4 seja a base ortogonal obtida a partir de B pela aplicação do processo de ortogonalização de Gram-Schmidt. Se v 4 = ( - 1,3 , 1,1 ) e w 4 = ( - 2,1 , 0,1 ) , então p r o j [ w 1 , w 2 , w 3 ]   v 4 é igual a:

a )   ( 1,1 , 2,1 )

b )   2,1 , 1,3

c )   ( 1,2 , 1,0 )

d )   ( - 1,2 , - 1 , - 4 )

e )   ( 0,1 , 1 , - 1 )

Ver solução completa

Questão 35

Seja W = a , b , c , d , e , f a = 2 e - 3 b , c = b - 4 a , d = 0 um subespaço de R 6 . A dimensão de W é igual a:

( a ) 2

( b ) 3

( c ) 4

( d ) 5

Ver solução completa

Questão 36

Considere a base B = {   1 ,   x - 1 ,   x - 1 2 ,   x - 1 3 } de P 3 ( R ) e seja p = x 3 + x 2 - 4 x - 2 ∈ P 3 ( R ) . Se a , b ,   c ,   d ∈ R são tais que p = a , b , c , d B , então a + b + c + d vale

Escolha uma opção:

  1. - 7
  2. - 2
  3. 2
  4. - 7
  5. - 5
  6. - 10
  7. 10
  8. 5

Ver solução completa

Questão 37

Sejam v 1 , v 2 , v 3 vetores de R 4 e seja V = v 1 , v 2 , v 3 o subespaço gerado por estes vetores. O conjunto dos possíveis valores para a dimensão de V é:

a   0,1 , 2,3

b   0,1 , 2,3 , 4

c   3

d   4

Ver solução completa

Questão 38

Considere as seguintes informações:

  1. Se V for espaço vetorial munido de um produto interno 〈 ⋅ ,   ⋅ 〉 , S for um subespaço de V , v for elemento de S , w for um elemento de V e v , w = 0 , então w ∈ S ⊥ .
  2. Se V for um espaço vetorial munido de um produto interno e S e T forem subespaços de V , então S ⊥ + T ⊥ ⊂ S ∩ T ⊥ ;
  3. Existem números reais distintos a ,   b   e   c tais que a base 1 ,   t ,   t 2 do espaço vetorial P 2 R é ortogonal com respeito ao produto interno definido por   p , q   = p a q a + p b q b + p c q c , para todos p , q ∈ P 2 R .

Escolha uma opção:

  1. Apenas a afirmação III é verdadeira;
  2. Todas as afirmações são falsas;
  3. Apenas a afirmação II é verdadeira;
  4. Apenas as afirmações I e III são verdadeiras;
  5. Apenas as afirmações I e II são verdadeiras;
  6. Todas as afirmações são verdadeiras;
  7. Apenas as afirmações II e III são verdadeiras;
  8. Apenas a afirmação I é verdadeira;

Ver solução completa

Questão 39

Seja W = a , b , c , d , e , f e = f - 3 a , c = 0 , d = 2 f + 3 e um subespaço de R 6 . A dimensão de W é igual a:

( a ) 5

( b ) 4

( c ) 2

( d ) 3

Ver solução completa

Questão 40

Se F = v 1 , v 2 , v 3 é um conjunto gerador de S , onde S é o conjunto de soluções de

- 2 x + 2 y + 2 z + 2 w = 0                                                                 2 y + 2 w = 0

então:

( a ) F pode ser 2,0 , 2,0 , 1,1 , 1,1 , 4,0 , 4,0 .

( b ) F pode ser 2,0 , 2,0 , 0 , - 2,0 , 2 , 2 , - 2,2 , 2 .

( c ) F pode ser 0 , - 2,0 , 2 , 2,2 , 2,2 , 0,2 , 0 , - 2 .

( d ) Qualquer dois vetores de F formam uma base para S .

Ver solução completa

Questão 41

Seja V um espaço vetorial de dimensão n , então é VERDADE que:

( a ) Todo subconjunto linearmente independente de V gera V .

( b ) Todo subconjunto gerador de V é linearmente independente.

( c ) Todo subconjunto de V com mais do que n vetores é linearmente dependente.

( d ) Nem todo subconjunto de V com n vetores linearmente independentes é uma base de V .

Ver solução completa

Questão 42

01) Considere o espaço vetorial R 3 munido de um produto interno ⟨ ⋅ , ⋅ ⟩ com respeito ao qual a base:

B = { 1,0 , 1 ,   0,1 , 1 ,   0,1 , 0 }

seja ortonormal. Temos que ⟨ 1,2 , 3 ,   1,2 , 3 ⟩ é igual a:

a) 6 ;

b) 35 ;

c) 14 ;

d) 1 ;

e) 5 ;

Ver solução completa

Questão 43

Seja A = 1 - 1 - 1 0 2 0 1 3 1 0 2 0 4 2 4 0 2 6 1 - 3

(b) Determine bases para o espaço linha e para o espaço coluna de A e suas dimensões.

Ver solução completa

Questão 44

Encontre a matriz de mudança de base da base β = 1 - 2 t + t 2 ; 3 - 5 t + 4 t 2 ; 2 t + 3 t 2 para a base canônica C = 1 , t , t 2 , e a matriz mudança de base da base canônica C para a base β

Ver solução completa

Questão 45

Seja A B C um triângulo equilátero de lado unitário no espaço E 3 e seja v → ∈ V 3 um vetor unitário que seja ortogonal aos vetores A B →   e   A C → . Se

w → = 2 A B → + A C → + 2 v →       e       z → = A B → + A C →

Então as coordenadas de p r o j z → w → na base A B → , A C → , v → são:

a )   4 3 , 4 3 , 0

b )   4,4 , 0

c )   2,1 , 3

d )   3 2 , 3 2 , 0

e )   - 1,2 , 0

Ver solução completa

Questão 46

Seja ξ uma base de V 3 ,   a um número real e sejam v → , w → e z → os vetores definidos por:

v → = 2,0 , 1 ξ ,     w → = - 1,0 , 2 ξ ,     e     z → = 0 , a , 1 ξ .

Considere as seguintes informações:

  1. v → e w → são ortogonais;
  2. O conjunto v → ,   w → ,   v - p r o j v →   w → não é uma base de V 3 ;
  3. Se z → não é ortogonal nem a v → nem a w → , então o conjunto

p r o j v →   z → ,   p r o j w →   z → ,   z →

É linearmente dependente se, e somente se, a = 0

Assinale a alternativa correta:

  1. Apenas as informações (I) e (II) são necessariamente verdadeiras;
  2. Nenhuma das afirmações é necessariamente verdadeira;
  3. Todas as afirmações são necessariamente verdadeiras;
  4. Apenas as afirmações (I) e (II) são necessariamente verdadeiras;
  5. Apenas as afirmações (II) e (III) são necessariamente verdadeiras.

Ver solução completa

Questão 47

Considere no espaço E 3 um cubo de arestas unitárias cujos vértices são A , B , C , D , E , F , G , H em que H G F E ,   H E A D ,   H G C D   são faces desse cubo, como ilustrado na figura abaixo:

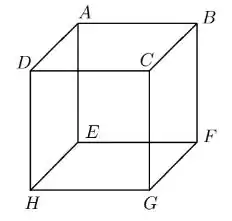
Assinale a alternativa contendo uma afirmação F A L S A :

a ) o conjunto A D → , A B → , A E → é uma base ortonormal de V 3 ;

b )   o produto escalar de A G → com A F → é igual a - 1 ;

c ) o conjunto A F → , A G → , A H → é linearmente independente;

d ) A G → + H E → + F D → = B C → ;

e ) o conjunto A D → , G C → , H G → é uma base de V 3 e as coordenadas do vetor A G → nessa base são 1 , - 1,1 .

Ver solução completa

Questão 48

Considere no espaço E 3 um prisma com faces triangulares A B C e D E F , em que A D , B E   e   C F são arestas desse prisma, como ilustrado na figura abaixo:

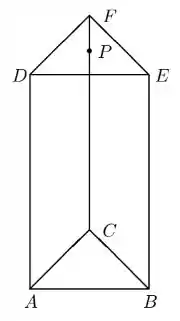
Seja P o ponto do segmento C F tal que C P → = 5 P F → . A soma das coordenadas do vetor D P → na base A B → , A C → , A F → é igual a:

a ) - 1 6 ;  

b ) 1 6

c )   0

d ) 4 3 ;  

e )   1

Ver solução completa

Questão 49

Sejam a , b ∈ R e ϵ uma base de V 3 . Considere os vetores:

v 1 → = - 1,3 , a ϵ ,     v 2 → = 2 , - 1,1 ϵ ,     v 3 → = 1,2 , 1 ϵ ,     w → = b , 2 b , 1 ϵ

Temos que o vetor w → é uma combinação linear dos vetores v 1 → ,   v 2 → , e v 3 → se, e somente se:

  1. a b ≠ 1
  2. a + b = 0
  3. a = b
  4. a + 2 b = 0
  5. a ≠ 0   ou b = 1

Ver solução completa

Questão 50

Seja B uma base ortonormal de V 3 e considere os vetores:

v → = 1 , - 1,2 B     e       w → = 3 , - 1,1 B

Seja z → o vetor paralelo a v → tal que w → - z → seja ortogonal a v → . A norma do vetor 2 z → - w → é igual a:

a )   11

b )   10

c )   12

d )   √ 7

e )   √ 8

Ver solução completa

Questão 51

Seja a ∈ R e considere os vetores

u 1 → = 1 , - a , - 1 B ,     u 2 → = a , 1 , - 1 B ,     u 3 → = 1,1 , 1 B

Em que B é uma base de V 3 . Pode-se afirmar que:

a )   u 1 → , u 2 → , u 3 →   é   u m a   b a s e   d e   V 3 ;

b )   u 1 → , u 2 → , u 3 →   é   u m a   b a s e   d e   V 3   s e ,   e   s o m e n t e   s e ,   1 ≤ a < 3

c )   u 1 → , u 2 → , u 3 →   é   u m a   b a s e   d e   V 3   s e ,   e   s o m e n t e   s e ,   - 2 < a < - 1

d )   u 1 → , u 2 → , u 3 →   é   u m a   b a s e   d e   V 3   s e ,   e   s o m e n t e   s e ,   3 ≤ a < 5

e )   u 1 → , u 2 → , u 3 →   é   u m a   b a s e   d e   V 3   s e ,   e   s o m e n t e   s e ,   5 ≤ a < 7

Ver solução completa

Questão 52

Seja B uma base de V 3 e sejam a , b   ∈ R . Considere os vetores

u → = 1,0 , 1 B ,     v → = b , 1,1 B ,     w → = 1,1 , 0 B ,     z → = 2 , a , 2 B

Sabendo que z → é combinação linear de u → , v → , w → ,   está correto afirmar que

A   a ≠ 0 .

B   b ≠ 2 .

C   s e   b = 2 ,   e n t ã o   a = 0 .

D   b = 2   e   a = 0 .

E   a b = 0 .

Ver solução completa

Questão 53

Seja B   uma base de V 3 e seja a   ∈ R . Considere as seguintes afirmações sobre os vetores u → = a , 1,1 B , v → = 1 , a , - a B ,   w → = 1 , a , - 1 B .

I .   S e   a ≠ 1 ,   e n t ã o   u → , v → , w →   é   u m a   b a s e   d e   V 3 .

I I .   O   c o n j u n t o   u → , v →   é   l i n e a r m e n t e   i n d e p e n d e n t e   p a r a   t o d o   a ∈ R  

I I I .   S e   a ≠ 1 ,   e n t ã o   u → , w →   é   l i n e a r m e n t e   i n d e p e n d e n t e .    

Ver solução completa

Questão 54

Seja B uma base de V 3 e seja a ∈ R . O intervalo no qual está o número a para que os vetores u → = a , 1 , a + 1 B , v → = 1,2 , - a B e w ��� = 1,1 , 1 B formem um conjunto linearmente dependente é:(a) ] 13 , + ∞ [

(b) ] 11 , - 3 ]

(c) ] - ∞ , - 11 ]

(d) ] - 3,5 ]

(e) ] 5 , 13 ]

Ver solução completa

Questão 55

Seja B uma base de V 3 . Considere os vetores

v 1 → = 1,1 , 0 B ,     v 2 → = 0,1 , - 1 B ,     v 3 → = 2,3 , - 1 B

Se a , b   ∈ R são tais que 2 v 1 → + a v 2 → + b v 3 → =   0 → , então a b é igual a

Ver solução completa

Questão 56

Seja u → ,   v → ,   w → um conjunto linearmente independente em V 3 e considere a base ρ = v → - u →   , v → - w → , u → de V 3 . Se ( a , b , c ) são as coordenadas de u → + 2 v → + 3 w → na base ρ , então a + b + c é igual a:

Ver solução completa

Questão 57

Seja { u → , v → , w → } uma base de V 3 . Considere as seguintes afirmações:

I .   { u → + x → , v → + x → , w → + x → } é linearmente independente, qualquer que seja x →   ∈ V 3

I I .   { u → , u → + v → , u → + v → + w → } é linearmente independente

I I I .   { v → + w → , u → + w → , u → + v → } é linearmente independente

Está correto apenas o que se afirma em

Ver solução completa

Questão 58

Seja ε uma base ortonormal de V 3 e seja λ ∈ R . Considere os vetores

f 1 = - λ , 0,4 ε

f 2 = 0,1 , 0 ε

f 3 = 5,0 , - λ ε

Sabendo que f 1 , f 2 , f 3 é uma base de V 3 com orientação oposta à de ε e que os vetores λ , - 4,6 ε e 2 λ , λ , - 5 ε são ortogonais, conclui-se que λ é igual a

Ver solução completa

Questão 59

Considere no espaço E 3 um cubo cujos vértices são A , B , C , D , E , F , G , H em que A B C D ,   A D H E ,   A B F E   são faces desse cubo, como ilustrado na figura abaixo:

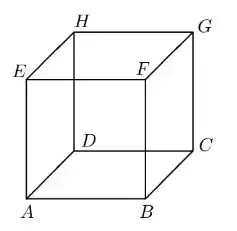
Seja B e C as bases de V 3 dadas por:

B = D A → , D C → , D H →     e     C = D E → , B D → ,   D G → .

Se M B C é a matriz real 3 x 3 tal que

M B C v → C = v → B ,

Para todo v → ∈ V 3 , então o determinante de M B C é igual a:

a )   1 ;

b ) - 1 ;

c )   3 ;

d )   2 ;

e ) - 2 .

Ver solução completa

Questão 60

Suponha que π 1   e   π 2 são planos cuja interseção é a reta r. Sejam n 1 →   e   n 2 → vetores não-nulos tais que n 1 → ⊥ π 1 e n 2 → ⊥ π 2 , e seja v → um vetor não-nulo paralelo a r. Considere as seguintes afirmações:

  1. Os vetores v →   e   n 1 →   ⋀     n 2 → são paralelas;
  2. B = { n 1 → , n 2 → , v → } é um base ortogonal de V 3 ;
  3. Os vetores v → ,   v →   ⋀ n 1 →   e   v → ⋀   n 2 → são linearmente independentes.

Ver solução completa

Questão 61

Considere as seguintes afirmações:

I   S e   B = u 1 → , u 2 → , u 3 → é base de V 3 e x → =   α 1 u 1 → + α 2 u 2 → + α 3 u 3 →   ∈ V 3 , então α 1 = x → , u 2 → , u 3 → u 1 → , u 2 → , u 3 →  

I I   S e   u → ,   v →   ,   w → ∈ V 3 ,   e n t ã o   u → ∧ v →   ∙ w → = u → ∙ v → ∧ w → ;

I I I   S e   u → , v → , w →   ∈ V 3 ,   e n t ã o   u → ∧ v → ∧ w → = u → ∧ ( v → ∧ w → )

Ver solução completa

Questão 62

Seja B = { u → , v → , w → } uma base ortonormal positiva de V 3 . x → = a , b , c B   é a solução da equação x → ∧   u → ∧ x → ∧ v → = 36 w → , então a soma a + b + | c | é igual a:

Ver solução completa

Questão 63

Se B = { u → , v → , w → } é base de V 3 , sabemos que C = { 1 2 u → + v → , 1 2 v → + w → , 1 2 w → + u → } também é base de V 3 . Se x → = a , b , c B , então é correto afirmar que:

Ver solução completa

Questão 64

Calcule a primeira coordenada do vetor 1 ,   2 ,   3 na base β = 1 ,   1 ,   1 ,   1 ,   - 2 ,   1 ,   1 ,   0 ,   - 1 :

  1. 3 6 .
  2. 2.
  3. 2 3 .
  4. 0 .

Ver solução completa

Questão 65

Considere as afirmações abaixo:

(I) 1,2 , 3 , 2,5 , 8 , 3,5 , 8 é uma base de R 3 .

(II) 1,1 , 2 , 2,3 , 2 , 3,5 , 2 é gerador de R 3 .

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Ver solução completa

Questão 66

Os vetores v 1 → = ( 1 ,   2 ,   3 ) , v 2 → = ( 3 ,   2 ,   1 ) e v 3 → = ( 2 ,   3 ,   1 ) geram o vetor v 4 → = ( 7 ,   7 ,   10 ) através de uma combinação linear:

I - Existe outra combinação linear de v 1 → , v 2 →   e   v 3 → que gera v 4 →

II - Qualquer vetor ( a ,   b ,   c ) pode ser gerado por v 1 → , v 2 →   e   v 3 →

(a) I é verdadeira e II é falsa

(b) Ambas são verdadeiras

(c) I é falsa e II é verdadeira

(d) Ambas são falsas

Ver solução completa

Questão 67

Seja   T :   M 2 × 2   R → P 2 R a transformação linear dada por T a b c d = a + b + c x + c + 2 d x 2 , α = 1 0 1 0 , 1 0 0 1 , 1 1 0 0 , 0 0 1 0   e β = { x ,   1 - x 2 , 2 } base de P 2 ( R ) .

a)Mostre que α é base de M 2 × 2   R .

Ver solução completa

Questão 68

Seja ϵ   uma base ortonormal de V 3 e considere os vetores:

v → = 1 , - 1,1 ϵ ,     w → = - 1,1 , 1 ϵ ,     z → = 1,2 , - 1 ϵ

Se a , b , c ∈ R são tais que o vetor x → = a , b , c ϵ é ortogonal a v → e w → e se p r o j z →   x →   =     z → , então a + b + c é igual a:

  1. 2 6
  2. 4
  3. 3
  4. 0
  5. -1.

Ver solução completa

Questão 69

Sejam E = e 1 , e 2 , e 3 e F = f 1 , f 2 , f 3 bases de V 3 tais que F é ortonormal e

f 1 = e 1 + e 2 - e 3 f 2 = e 2 - e 3 f 3 = 2 e 2 - e 3

Se v = 0,1 , 1 F e u = 1,1 , 1 E , então p r o j v u é igual a

Ver solução completa

Questão 70

Considere fixada uma orientação em V 3 , e seja β uma base ortonormal positiva de V 3 . Considere os vetores

v = 1,2 , 0 β

w = 1,0 , 1 β

Sabendo que

- u ∈ V 3 é ortogonal a v e a w

- u = 3

- { u , v , w } é uma base positiva de V 3

Se u = a , b , c β então a + b + c é igual a

Ver solução completa

Questão 71

Seja β uma base ortonormal de V 3 e seja u o vetor que satisfaz as seguintes condições:

- u = 2 6

- u é ortogonal a - 1,1 , 0 β

- O ângulo entre u e - 1 , - 1,0 β mede 30 °

- u forma um ângulo obtuso com 0,0 , 1 β

Se u = a , b , c β , então a + b + c é igual a

Ver solução completa

Questão 72

Considere o espaço vetorial M 2 × 2 R , e os subconjuntos

W 1 = a b c d ∈ M 2 × 2 R ; a = c   e   b . d = 0

W 2 = a b c d ∈ M 2 × 2 R ; a + b - c + 2 d = 0   e   b + c = 0

a Verifique se W 1 é subespaço de V .

b Verifique se W 2 é subespaço de V , determine uma base para W 2 .

Ver solução completa

Questão 73

Seja β = u → , v → , w → uma base para o espaço vetorial V e seja W o espaço gerado por β . Considere as seguintes afirmações abaixo e assinale a resposta CORRETA:

  1. Todo vetor de V é vetor de W
  2. Existe um vetor em W que não está em V

a   Ambas são falsas.

b   I é verdadeira e I I é falsa.

c   Ambas são verdadeiras.

( d ) I I é verdadeira e I é falsa.

Ver solução completa

Questão 74

  1. Considere o conjunto:

W = { ( a + c ,   a + b - c ,   b - 2 c ,   - a + b - 3 c ) | a , b , c ∈ R }

  1. Determine uma base para W .

Ver solução completa

Questão 75

Prove que se o conjunto de vetores ( u → , v → , w → ) forma uma base para o espaço, então o conjunto ( u → + v → ,   u → - v → ,   w → - 2 u → ) também forma uma base para o espaço.

Ver solução completa

Questão 76

São dados três vetores u → , v → ,   w →   ∈ V 3 , e sabe-se que a medida do ângulo entre u →   e   v →   é π 4 , que w →   é ortogonal a u →   e   a   v → , e que ( u → , v → , w → ) é base negativa de V 3 . Além disso, sabe-se que u → = 2 2 , v → = 1   w → = 4 . Segue-se desses fatos que [ u → , v → , w → ] é igual a:

Ver solução completa

Questão 77

Seja V um espaço vetorial de dimensão 2 e S = { v 1 → ,   v 2 → ,   v 3 → } um conjunto gerador de V , com todos os vetores distintos entre si.

Sejam A = { v 1 → ,   v 2 → } e B = { v 2 → ,   v 3 → } e C = { v 1 → ,   v 3 → } .

Assinale a alternativa FALSA:

( a ) A ,   B e C podem todos ser bases de V

( b ) A ,   B e C podem todos ser conjuntos geradores de V

( c ) A ,   B e C podem todos ser conjuntos linearmente independentes ( L I )

( d ) A ,   B e C podem todos ser conjuntos linearmente dependentes ( L D )

Ver solução completa

Questão 78

A única afirmativa verdadeira é:

( a ) Se um conjunto é linearmente dependente então ele gera o espaço inteiro.

( b ) Todo subconjunto de um conjunto linearmente dependente é linearmente dependente.

( c ) Nenhum conjunto linearmente independente gera o espaço inteiro.

( d ) Todo subconjunto de um conjunto linearmente independente é linearmente independente.

Ver solução completa

Questão 79

Seja E = ( e 1 → ,   e 2 → ,   e 3 → ) uma base e considere os vetores

f 1 → = e 1 → + e 2 → + e 3 →

f 2 → = - e 2 → + 2 e 3 →

f 3 → = - e 3 →

a) Verifique que F = ( f 1 → ,   f 2 → ,   f 3 → ) é base.

b) Calcule a e b de modo que, para os vetores u → = 1 ,   - 1 ,   4 E e v → = 1 ,   a ,   b F , a sequência ( u → ,   v → ) seja L.D.

Ver solução completa

Questão 80

Seja H o subespaço definido por

2 , - 1,1 , 2 , - 2,2 , 4 , - 6,6 , 0 , - 3,3

Qual dos conjuntos abaixo é base de H ?

a   2 , - 1,1 , 2 , - 2,2 , 4 , - 6,6 , 0 , - 3,3

b   2 , - 1,1 , 2 , - 2,2

c   2 , - 1,1 , 2 , - 2,2 , 4 , - 6,6

( d ) 2 , - 1,1

Ver solução completa

Questão 81

Em E 3 , sejam π 1   e   π 2 planos cujas interseção é uma reta r. Sejam n 1 →   e n 2 → vetores não-nulos de V 3 tais que n 1 → ⊥ π 1 e n 2 → ⊥ π 2 , e seja v → ∈ V 3 um vetor não-nulo paralelo a r. Considere as seguintes afirmações:

I .   O s   v e t o r e s   v →   e   n 1 → ∧ n 2 → são paralelos

I I .   B = n 1 →   ,   n 2 → , v → é uma base ortogonal de V 3

I I I .   O   c o n j u n t o   v → , v →   ∧   n 1 → ,   v →   ∧   n 2 →   é linearmente independente

Está correto o que se afirma em

a )     I   e   I I ,   a p e n a s

b )   I , I I   e   I I I

c )   I   e   I I I ,   a p e n a s

d )   I I ,   a p e n a s

e )   I I I ,   a p e n a s

Ver solução completa

Questão 82

Considere os polinômios:

p 1 t = - 1 - t + 4 t 2 - 5 t 3 , p 2 t = 1 + 4 t - t 2 + 3 t 3 e p 3 t = 1 + t - 4 t 2 + 4 t 3 .

Assinale a alternativa em que o polinômio p 4 é tal que { p 1 , p 2 , p 3 , p 4 } é uma base de P 3 R :

  1. p 4 t = 1 + 3 t - 2 t 2 + 3 t 3 ;
  2. p 4 t = t 3 ;
  3. p 4 t = t + t 2 ;
  4. p 4 t = 1 + 4 t - t 2 ;
  5. p 4 t = 5 t 2 + 5 t 3 .

Ver solução completa

Questão 83

Sejam V = P 3 R = a 0 + a 1 x + a 2 x 2 + a 3 x 3     a i   ∈ R } , B = { 1 , x , x 2 , x 3 } a base canônica e S = { 1,0 , 1,0 B , 0,1 , 0,1 B , 0,1 , 1,0 B } . Nestas condições se o vetor u = α , β , 2 , - 1 B é tal que S   ∪ u   é L.D., então α + β   pertence ao intervalo

Ver solução completa

Questão 84

Se B = u → , v → , w → é uma base de V 3 , sabemos que

τ = 1 2 u → + v → , 1 2 v → + w → , 1 2 w → + u →

Também é base de V 3 . Dado x →   ∈   V 3 , se x → = a , b , c B , então as coordenadas de x → em relação à base τ são

a )   ( a - b , b - c , c - a )

b )   ( a + 2 b - c , - a + 2 b + c , a - 2 b + c )

c )   ( a + b - c , - a + b + c , a - b + c )

d )   ( 2 a + b - c , - a + 2 b + c , a - b + 2 c )

e )   a + b , b + c , c + a

Ver solução completa

Questão 85

Seja β uma base ortonormal de V 3 . Considere os vetores

x → = 2,2 , 1 β

u → = 1,0 , 1 β

v → = 0 , - 1,1 β

Sejam y → ,   z → ∈ V 3 tais que

- x → = y → + z →

- { u → , v → , y → } é linearmente dependente, e

- z → é ortogonal a u → e a v →

Se z → = a , b , c β , então a + b + c é igual a

Ver solução completa

Questão 86

Considere os vetores de R 3

u 1 = 1 ,   1 ,   2 ,     u 2 = 2 ,   0 ,   1

(escritos na base canônica) e a transformação linear

T : R 3 → R 3 ,     T v = v . u 1 u 1 + v . u 2 u 2  

  1. Determine a matriz de T na base canônica.
  2. Determine uma base da imagem de T .
  3. Considere o plano vetorial

V : x + y + 2 z = 0

Determine uma base do subespaço T V , a imagem do plano V pela transformação linear T .

Ver solução completa

Questão 87

É uma base do núcleo de:

4 4 3 3 2 2 1 1

(a) { - 1,0 , 0,4 , - 1,0 , 3,0 , - 1,2 , 0,0 }

(b) { 1,0 , 0 , - 4 , 0,1 , 0 , - 3 , 0,0 , 1 , - 2 }

(c) { 1,0 , 0 , - 4 , 1,0 , - 3,0 , 1 , - 2,0 , 0 }

(d) { 0,1 , 0 , - 4 , 1,0 , - 3,0 , - 1 , - 2,0 , 0 }

Ver solução completa

Questão 88

Um subespaço W ⊂ R 3 admite a base

β = 1,1 , 2 , 1 , - 1,1

Qual dos conjuntos abaixo também é base de W ?

a   2,0 , 3 , 2,0 , 1

b   1,3 , 3 , 1,1 , 2

c   0 , - 2,1 , 0 , - 2 , - 1

d   1,1 , 2 , 1,1 , 0

Ver solução completa

Questão 89

Seja H o subespaço definido por

2,1 , - 1 , 2 , - 1,2 , 2 , - 7,11 , - 2,5 , - 8

Qual dos conjuntos abaixo é base de H ?

a   2,1 , - 1 , 2 , - 1,2

b   2,1 , - 1

c   2,1 , - 1 , 2 , - 1,2 , 2 , - 7,11

d   2,1 , - 1 , 2 , - 1,2 , 2 , - 7,11 , - 2,5 , - 8

Ver solução completa

Questão 90

Assinale a alternativa CORRETA:

( a ) 1,0 , 1,1 , 1 , - 1 não é um conjunto gerador de R 2

( b ) 1,0 , 0,1 e 1,1 , 1 , - 1 são bases de R 2

( c ) 1,1 , 1 , 2,2 , 2 , 3,3 , 3 é um conjunto gerador de R 3

( d ) 1,2 , 3 , 4,5 , 6 , 7,8 , 9 é uma base de R 3

Ver solução completa

Questão 91

Considere as seguintes afirmações sobre um espaço vetorial E com produto interno , :

I   S e   S 1   e   S 2   s ã o   s u b e s p a ç o s   d e   E   t a i s   q u e   S 1 ⊂ S 2 ,   e n t ã o   S 1 ⊥ ⊂ S 2 ⊥

I I   S e   u 1 , u 2 , u 3   é   u m a   b a s e   d o   s u b e s p a ç o   S   d e   E ,   e n t ã o

p r o j S v = p r o j [ u 1 ] v + p r o j [ u 2 ] v + p r o j [ u 3 ] v ,

Qualquer que seja v   ∈ E

I I I   S e   E = u 1 ,   … ,   u n   e   v ∈ E   é   t a l   q u e   v , u j = 0 ,   p a r a   t o d o   j = 1 , … , n   e n t ã o   v = 0 V

Está correto o que se afirma em

a   I   e   I I I ,   a p e n a s

b   I I I ,   a p e n a s .

c   I ,   I I   e   I I I .

d I I ,   a p e n a s

e   I   e   I I ,   a p e n a s

Ver solução completa

Questão 92

Sejam n um inteiro positivo e 𝑉     um espaço vetorial real de dimensão 𝑛   munido de um produto interno. Sejam 𝐵   e   𝐶 bases de 𝑉   e   𝑀   ∈   𝑀 𝑛 𝑅 a matriz tal que 𝑀 𝑣 𝐵 = 𝑣 𝐶 para todo 𝑣   ∈   𝑉   . Pode-se afirmar que:

(a) se as bases 𝐵   e   𝐶 forem ortonormais, então a transposta da matriz 𝑀   será igual a − 𝑀  

(b) se as bases 𝐵   e   𝐶 forem ortonormais, então a transposta da matriz 𝑀   será igual à inversa de 𝑀  

(c) se as bases 𝐵   e   𝐶 forem ortogonais, ent ̃ao a transposta da matriz 𝑀   será igual a − 𝑀  

(d) se as bases 𝐵   e   𝐶 forem ortogonais, então a transposta da matriz 𝑀   será igual à inversa de   𝑀  

(e) se as bases 𝐵   e   𝐶 forem ortonormais, então a transposta da matriz 𝑀   será igual a 𝑀  

Ver solução completa

Questão 93

Considere o subespaço vetorial

F = { a 0 + a 1 x + a 2 x 2   ∈ P 2 :   a 0 - 2 a 1 + 4 a 2 = 0 }

a) Obtenha uma base para F .

b) Obtenha uma base α = { u 1 ,   u 2 ,   u 3 } para o P 2 tal que u 1 e u 2 sejam elementos de F .

Ver solução completa

Questão 94

Indique se cada afirmação abaixo é verdadeira ou falsa. Justifique.

(c) O conjunto { 1 + x , - x + x 2 , 2 + x 2 } não é base para o P 2 R .

Ver solução completa

Listas de Exercícios Resolvidos

Lista de Introdução às EDO'sLista de Subespaços VetoriaisLista de ElipsesLista de Parábolas Lista de Ângulos entre RetasLista de Combinação LinearLista de Posições Relativas de RetasLista de Reflexão OrtogonalLista de Expressão Analítica de uma TLLista de Complemento Ortogonal e Soma Direta

Principais Conceitos de Álgebra Linear e Geometria Analítica

Equação da Esfera