Dado o triângulo ABC, sejam P, O e R pontos tais que . Prove que, se , então B, C e R são colineares.
Passo 1
Bora lá!
O exercício condiciona que , então temos que buscar alguma igualdade que invalide caso , certo? E devemos usar as colinearidades subentendidas para representar a figura:
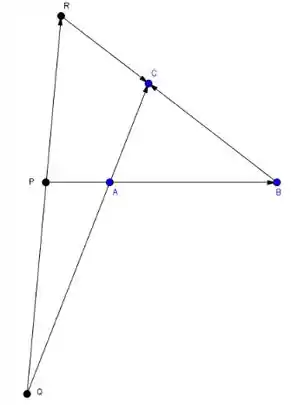
Passo 2
Devemos achar as relações que envolvam os lados do triângulo em função de , e que envolvam R:
Passo 3
Como , podemos cortar um com o outro, beleza?
Aplicando o restante das relações relativas a P, Q, e R deduzidas, temos:
Passo 4
Concluímos que o vetor é múltiplo de , portanto B, C e R são pontos colineares, desde que .
Resposta
Ei, a resposta está no passo a passo :)