Sejam o foco, o parâmetro e a diretriz de uma parábola . Prove que

pertence a região focal de se, e somente se,

pertence a região côncava determinada por se, e somente se,

A equação de uma parábola horizontal segue uma equação igual a:

Na letra nós teremos algo do tipo.

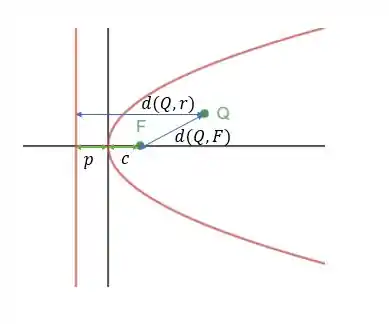
Onde é a direção do ponto para a reta diretriz e cada componente tem pontos e expressões iguais a:

Isso é, a reta diretriz é igual a , isso nos dá uma reta vertical em

Logo:

Onde:

Isso é a distância entre e o foco subtraída da distância entre o ponto e a reta nos dará um valor positivo que valerá:

Então:

Elevando os dois lados ao quadrado nós teremos:

Então temos que se teremos uma equação igual a e pertence a parábola. Se então:

Logo o ponto está na região fora da parábola portanto na região côncava então .