Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 48
Seja um ponto não pertencente a elipse , distinto da origem. Prove que
se é interior a elipse, existe em tal que é interior a
se é exterior a , existe em interior a
(lembre-se: um ponto é interior ao segmento se, e somente se, existe tal que e ).
Passo 1
O que a letra está retratando é algo desse nível aqui ó:
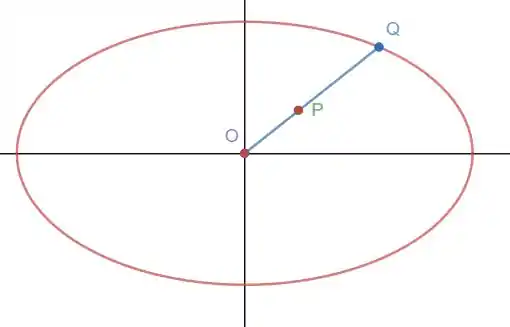
E que o segmento de reta está dentro de uma elipse com comportamento igual a:
Ou seja, para o ponto teremos a seguinte relação:
Onde esse será igual a 1, para as coordenadas e de q. Portanto quando e , então esse ficará restrito entre , uma vez que e assim como e sempre nos darão números positivos.
E como queremos mostrar que é interior ao segmento então:
Onde consideramos coincidente com , uma vez que queremos pelo menos um ponto onde esteja dentro do segmento , então sim deve estar entre zero e 1 para que a equação acima seja verdadeira.
Passo 2
Já se é externo nós iremos ter algo como:
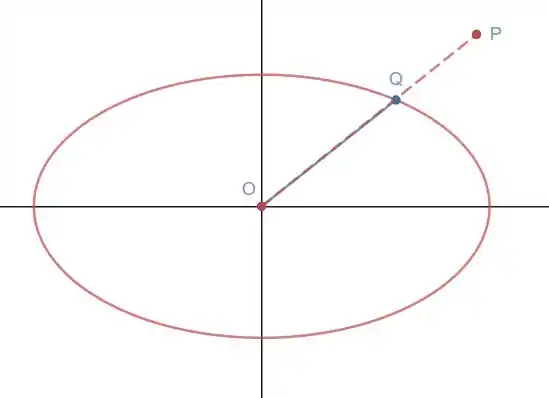
Então teríamos algo como:
Onde e . E com isso o valor de seria maior que um.
Resposta
Ei, a resposta está no passo a passo :)