Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 8.3 - Ex. 17

Sejam T : P 1 → R 2 a função definida pela fórmula

T p x = p 0 ,   p 1

  1. Encontre T ( 1 - 2 x ) .
  2. Mostre que T é uma transformação linear.
  3. Mostre que T é injetora.
  4. Encontre T - 1 ( 2 ,   3 ) e esboce seu gráfico.

Passo 1

Na letra (a) temos que encontrar T ( 1 - 2 x ) , como T p x = p 0 ,   p 1 , então p x = 1 - 2 x , e temos que encontrar p 0   e   p ( 1 )

p 1 = 1 - 2 1 = - 1

p 0 = 1 - 2 0 = 1

Logo T 1 - 2 x = ( 1 ,   - 1 )

Passo 2

Na letra (b), para mostrarmos que é uma transformação linear, precisamos verificar as duas propriedades

  1. T k v = k T ( v ) [Homogeneidade]
  2. T u + v = T u + T ( v ) [Aditividade]

Então para (i), temos

T p x = p 0 ,   p 1

T k p x = k p 0 ,   k p 1 = k p 0 ,   p 1

E para (ii), temos

T p x + q ( x ) = p 0 + q 0 ,   p 1 + q 1

Sendo h x = p x + q ( x )

T p x + q ( x ) = p 0 + q 0 ,   p 1 + q 1 ⇒ T h x = h 0 ,   h 1

Passo 3

Na letra (c), p ( x ) pertence a P 1 ,e é um polinômio de grau 1 do tipo a x + b , e pra transformação ser injetora, temos que n u l T = 0 , como T p x = p 0 ,   p 1 , precisamos encontrar um polinômio tal que

p 0 = p 1 = 0

Mas nosso polinômio de grau 1, só possui UMA raiz, então pra isso poder acontecer só se p x = 0 , logo n u l T = 0 e nossa transformação é injetora.

Passo 4

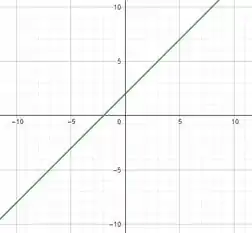
Na letra (d), pra encontrarmos T - 1 ( 2 ,   3 ) , temos que usar a forma a x + b do polinômio, já que

p 0 = a 0 + b = 2

p 1 = a 1 + b = 3

Logo, b = 2 e a = 1 , dessa forma a x + b se torna x + 2 , portanto T - 1 2 ,   3 = 2 + x e seu gráfico é

Resposta

  1. T 1 - 2 x = 1 ,   - 1 .
  2. Demonstração.
  3. Demonstração.
  4. T - 1 2 ,   3 = 2 + x .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

T 1 : R 2 → R 2 é a reflexão no eixo x e T 2 : R 2 → R 2 é a reflexão no eixo y . T 1 : R 2 → R 2 é a projeção ortogonal no eixo x e T 2 : R 2 → R 2 é a rotação anti-horária pelo ângulo θ . T 1 : R 3
Sejam T : R 2 → R 2 o operador linear dado pela fórmula T x ,y = ( x + k y ,- y ) . Mostre que T é injetor e que T - 1 = T , qualquer que seja o valor real de k .
Sejam T 1 : P 2 → P 3 e T 2 : P 3 → P 3 os operadores lineares dados pelas fórmulas T 1 p x = x p ( x ) eT 2 p x = p x + 1 Encontre fórmulas para T 1 - 1 x ,y , T 2 - 1 x ,y , T 2 ∘ T 1 - 1 ( x ,y ) V
Prove: se T : V → W for uma transformação linear injetora, então T - 1 : I m T → V é uma transformação linear injetora.
Seja T : R n → R n o operador linear definido pela fórmula T x 1 ,x 2 ,... ,x n = a 1 x 1 ,a 2 x 2 ,... ,a n x n Em que a 1 ,a 2 ,... ,a n são constantes.Sob quais condições T terá uma inversa?Supondo