Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 8.Exercícios Propostos - Ex. 25
Sejam e
. Mostre que a interseção de e é uma circunferência e calcule o seu centro e raio.
Passo 1
Galera, antes de mais nada vamos começar reduzindo as equações das esferas:
Com isso, descobrimos o raio e o centro da primeira esfera: e
Agora, descobrimos que o raio e o centro da segunda esfera são: e
Para mostrar que a interseção entre as duas esferas é uma circunferência, temos que mostrar que a distância entre os dois centros é menor que a soma dos raios das duas esferas. Então, vamos começar calculando a distância entre os centros:
Por outro, a soma dos raios é dada por:
Com isso, vemos que a distância entre os dois centros é menor que a soma dos dois raios. Assim, fica provado que a interseção é uma circunferência.
Passo 2
Como a interseção entre as esferas é uma circunferência, então temos que calcular o centro da circunferência e seu raio. Pode parecer complicado, mas o raciocínio é exatamente o mesmo de quando temos a interseção entre uma esfera e um plano. Nesse caso, a única dificuldade é determinar a distância entre um dos centros, vamos escolher o primeiro, e o centro da circunferência. Veja mais ou menos como essas esferas ficarão quando olhamos a figura “por cima”, ou seja, estamos vendo a projeção no plano xy:
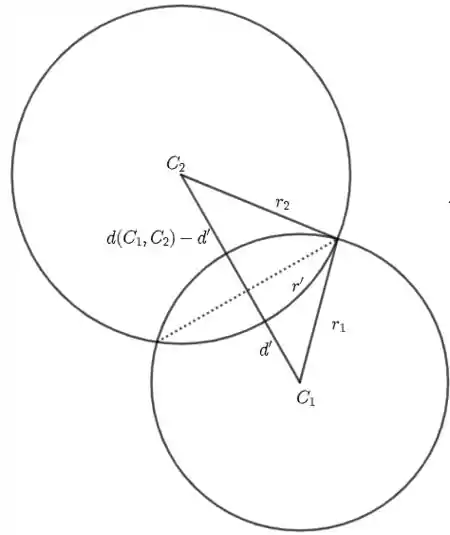
Devemos notar que temos dois triângulos retângulo, onde o raio da circunferência é um cateto comum dos dois. Então, nós temos duas relações a partir do teorema de Pitágoras:
Agora a gente subtrai a segunda equação da primeira:
Assim, conseguimos determinar a distância entre o centro 1 e o centro da circunferência. Agora só precisamos substituir os valores:
A partir dessa distância, podemos obter o raio da circunferência a partir da equação:
.
Passo 3
Beleza! Agora só falta calcular o centro da circunferência e, para isso, vamos usar o velho truque de utilizar uma reta ligando os pontos e . O vetor diretor dessa reta será
Assim, se considerarmos a reta saindo de , teremos as equações paramétricas . Temos que descobrir para qual valor de a reta se encontra no ponto . Nesse caso, temos um vetor que sai até cujo módulo vai ser igual a distância entre e :
Agora, substituímos esse valor no ponto :
Resposta
e