Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 13.Exercício - Ex. 15
Sejam , , e . Mostre que esses pontos são vértices de um trapézio e diga quais são as bases, os lados não-paralelos e as diagonais.
Passo 1
Temos que mostrar os pontos dados são vértices de um trapézio. Para isso, vamos achar todos os vetores possíveis entre os pontos:
Note que . Assim, achamos os lados paralelos do trapézio!
Passo 2
Perceba também que:
Visualizando a figura, temos
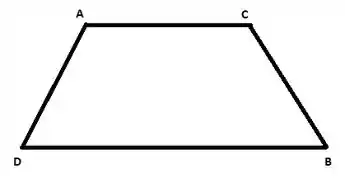
é a base maior, a base menor, e são os lados não paralelos e e são as diagonais.
Resposta
Demonstração.
Exercícios de Livros Relacionados
Mostre que { A 1 , A 2 , A 3 , A 4 } é uma base de M 22 e expresse A como uma combinação linear dos vetores da base. A 1 = 1 1 1 1 , A 2 = 0 1 1 1 , A 3 = 0 0 1 1 , A 4 = 0 0 0 1 , A = 1 0 1 0
Seja v → = ( 1 ,1 ,2 ,- 3 ,1 ) . Encontre todos os escalares k tais que k v → = 4 .
Seja v → = ( - 2 ,3 ,0 ,6 ) . Encontre todos os escalares k tais que k v → = 5 .
Encontre u → ⋅ v → , u → ⋅ u → e v → ⋅ v → . u → = 3 ,1 ,4 ,v → = ( 2 ,2 ,- 4 ) u → = 1 ,1 ,4 ,6 ,v → = ( 2 ,- 2 ,3 ,- 2 )
Encontre a norma de v → , um vetor unitário de mesma direção e sentido de v → e um vetor unitário de mesma direção e sentido oposto de v → . v → = ( 4 , - 3 ) v → = ( 2 ,2 ,2 ) v → = ( 1 ,0 ,2 ,1 ,3 )