Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 62d
Sejam e nao-nulos.
(d) Na treliça representada na Figura 9-9, a barra AB tem 20 metros de comprimento. Calcule a distância entre A e H
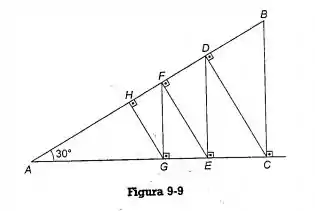
Passo 1
Bora lá!
Essa é a nossa trelição da questão
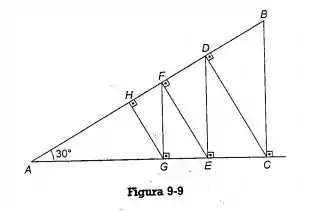
Para calcularmos a medida de , ou seja, o módulo do vetor , primeiramente, devemos notar que é a sexta projeção de, em ângulo de 30°.
Como assim? Vamos representar isso na nossa figura.
Passo 2
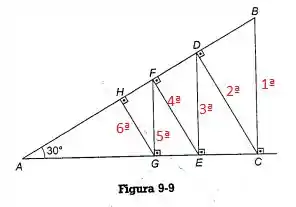
Beleza?
Dessa forma, tomaremos como base a fómula encontrada na letra (c) e substituiremos pelos dados que nós temos, portanto
Passo 3
Queremos a distância entre A e H, dessa forma, vamos calcular o módulo do vetor :
Resposta
Logo, .
Exercícios de Livros Relacionados
Determinar o vetor v → nos seguintes casos: v → é ortogonal ao eixo O x , v → = 2 , forma ângulo de 60 ° com o vetor j → e ângulo agudo com k → .
Mostrar que existe vetor cujos ângulos diretores são 30 ° , 90 ° e 60 ° , respectivamente, e determinar aquele que tem módulo 10 .
Para cada um dos pares de vetores u → e v → , encontrar a projeção ortogonal de v → sobre u → e decompor v → como soma de v → 1 com v → 2 , sendo v → 1 | | u → e v → 2 ⊥ u → . u → = 1,2 , - 2 e v → =
Sejam A 2,1 , 3 , B m , 3,5 e C 0,4 , 1 vértices de um triângulo (Figura 2.18 ) responda:Mostrar que A H - ⊥ B C - .
Sejam A 2,1 , 3 , B m , 3,5 e C 0,4 , 1 vértices de um triângulo (Figura 2.18 ) responda:Determinar o ponto H , pé da altura relativa ao vértice A .