Sejam e pontos distintos, pertencentes a superfície esférica de centro e raio . Mostre que todos os pontos interiores ao segmento são interiores a , e todos os pontos da reta , exteriores ao segmento , são exteriores a .

Considerando um centro na origem da esfera nós teremos:

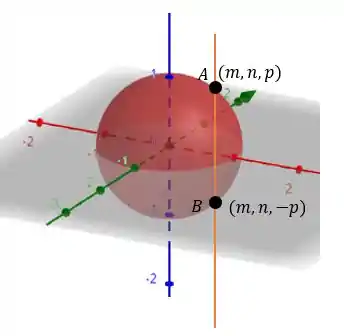
Considerando que a reta é paralela ao eixo , logo essa reta atravessa a esfera nas mesmas coordenadas em e porém em coordenadas em com valores inversos. Então pelo desenho fica tranquilo de ver que qualquer ponto dentro do segmento está dentro da esfera e qualquer ponto fora desse segmento estará fora da esfera também.

Uma forma de provar matematicamente o que estamos dizendo é que para uma esfera de equação tem raio de tanto para tanto para (que pertencem sei lá a uma reta , portanto qualquer ponto entre esses dois pontos terá um raio menor que (em relação ao seu centro), e qualquer ponto fora desse segmento terá um raio maior que 1 para o seu centro. Logo:

E como essa reta está paralela ao eixo , então se pegarmos um valor entre o segmento que terá um , logo:

E para um