Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 12.Exercício - Ex. 7
Sejam e pontos não-colineares. Exprima a distância de um ponto ao plano em função de .
Passo 1
Temos algo mais ou menos assim, olha:
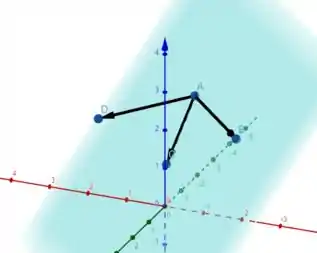
Vamos agora imaginar um paralelepípedo com base no plano e altura , ou seja, a distância de até o plano é a altura desse paralelepípedo.
Passo 2
Sabemos que o volume de um paralelepípedo é:
Onde e são as arestas da base e é a altura .
Como queremos encontrar , a distância de até o plano, temos:
Então, a altura do paralelepípedo é o volume dele dividido pela área da base.
Passo 3
A área da base do nosso paralelepípedo, ou seja, a área do nosso paralelogramo, é dada pelo produto vetorial:
E o volume do paralelepípedo é dado pelo produto misto
Então, a distância de até o plano, ou seja, a altura do paralelepípedo, será escrita como:
Resposta
Exercícios de Livros Relacionados
Encontre um vetor não nulo ortogonal ao plano que passa pelos pontos P ,Q ,R e calcule a área do trângulo P Q R . P 2,1 , 5 Q - 1,3 , 4 R 3,0 , 6
Use o produto misto para determinar se os pontos pertencem ao mesmo plano: A ( 1,3 , 2 ) B ( 3 , - 1,6 ) C ( 5,2 , 0 ) D ( 3,6 , - 4 )
Se v 1 ,v 2 ,v 3 são vetores não coplanares, sejam k 1 = v 1 × v 3 v 1 ∙ v 2 × v 3 k 2 = v 3 × v 1 v 1 ∙ v 2 × v 3 k 3 = v 1 × v 2 v 1 ∙ v 2 × v 3 (Esses vetores aoarecem no estudo de cristalografia.
Calcule o volume do paralelepípedo determinado pelos vetores a ,b e c . a =6,3 , - 1 b =0,1 , 2c =4 , - 2,5
Determine a área do paralelogramo com vértices em K ( 1 ,2 ,3 ) ,L ( 1 ,3 ,6 ) ,M ( 3 ,8 ,6 ) e N ( 3 ,7 ,3 ) .