A base do paralelepípedo na Figura 12-3 tem área 9. O ponto divide na razão , e a aresta , de comprimento , forma com o plano da base um ângulo de . Calcule , sabendo que está orientado por uma base dextra.
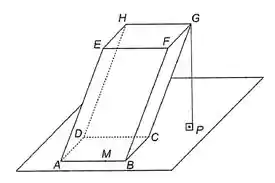
Passo 1
Sabemos que:
Onde é o ângulo que forma com .
Passo 2
Vamos pensar uma coisa: como são vetores diretores do plano da base, o produto vetorial deles é um vetor normal do plano não é? Então é paralelo a .
Qual o ângulo entre e ?
Como forma com o plano base, por análise de triângulo retângulo, vemos que ele forma com . Então:
Agora se a gente olhar a área da base, vamos ter:
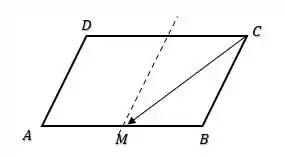
Isso quer dizer que podemos relacionar a área da base de com a área da outra base . De modo que:
Onde é a área que o enunciado nos valendo , sendo assim, segue que:
Passo 3
Portanto, como , de acordo com o enunciado, vale , obtemos que::
Então: