Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 12.4 - Ex. 33
Calcule o volume do paralelepípedo determinado pelos vetores e .
Passo 1
Nesse exercício devemos aplicar a seguinte noção para calcularmos o volume do paralelogramo. Seja um paraleograma qualquer como o descrito abaixo:
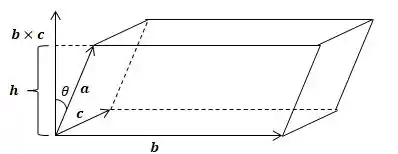
Volume de um pararelograma é dado por que no caso são:
Passo 2
Com a explicação basta fazermos contas para encontrarmos o resultado.
Resposta
Exercícios de Livros Relacionados
70. Determinar o valor de k para que os seguintes vetores sejam coplanares:a) a = 2 , - 1 , k ,b = 1,0 , 2 e c = k , 3 , k b) a = 2,1 , 0 ,b = 1,1 , - 3 e c = k , 1 , - k c) a = 2 , k , 1 ,b = 1,2 , k
69. Para que valor de m os pontos A m , 1,2 ,B 2 - 2 , - 3 ,C 5 , - 1,1 e D 3 , - 2 , - 2 são coplanares?
75. Calcular o volume do tetraedro A B C D , sendo dados:a) A 1,0 , 0 , B 0,1 , 0 , C 0,0 , 1 e D 4,2 , 7 b) A - 1,3 , 2 , B 0,1 , - 1 , C - 2,0 , 1 e D 1 , - 2,0 . Para este, calcular também a medida
75. Calcular o volume do tetraedro A B C D , sendo dados:a) A 1,0 , 0 , B 0,1 , 0 , C 0,0 , 1 e D 4,2 , 7 b) A - 1,3 , 2 , B 0,1 , - 1 , C - 2,0 , 1 e D 1 , - 2,0 . Para este, calcular também a medida
70. Determinar o valor de k para que os seguintes vetores sejam coplanares:a) a = 2 , - 1 , k ,b = 1,0 , 2 e c = k , 3 , k b) a = 2,1 , 0 ,b = 1,1 , - 3 e c = k , 1 , - k c) a = 2 , k , 1 ,b = 1,2 , k