Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 20
Dados , e , determine, em função de , e , os vetores e , sabendo que .
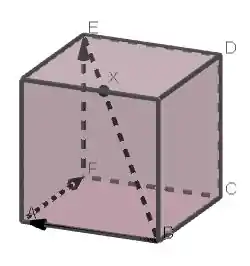
Passo 1
Fala, galerinha! Bora detonar mais uma questão?
Antes de mais nada, vamos desenhar os vetores e . Ficamos com a seguinte figura:
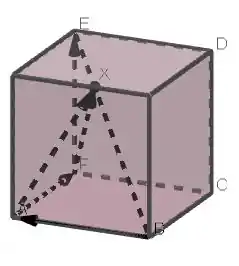
Aqui é a visão de outro ângulo:
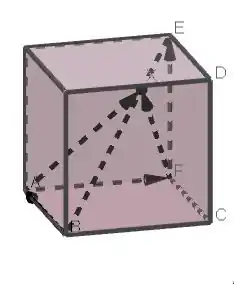
Nesse caso, vemos que
Passo 2
O enunciado já definiu que , mas e quanto a , e ? Bom, primeiramente temos que notar que , e . Essa sacada vai facilitar bastante os nossos cálculos. Agora, só temos que determinar e . No primeiro desenho, vemos que
Além disso,
Passo 3
Agora que já determinamos os quatro vetores que eram necessários, podemos substituir nas expressões encontradas lá no Passo 1:
Resposta
Exercícios de Livros Relacionados
Seja f uma função que faz correspondente a cada par de vetores v = ( a 1 ,b 1 ) , w = ( a 2 ,b 2 ) um numero real f v , w . (Noutras palavras tem-se uma função f :R 2xR 2 → R ). Suponha que f tem as s
Seja f uma função que faz correspondente a cada par de vetores v = ( a 1 ,b 1 ) , w = ( a 2 ,b 2 ) um numero real f v , w . (Noutras palavras tem-se uma função f :R 2xR 2 → R ). Suponha que f tem as s
Seja f uma função que faz correspondente a cada par de vetores v = ( a 1 ,b 1 ) , w = ( a 2 ,b 2 ) um numero real f v , w . (Noutras palavras tem-se uma função f :R 2xR 2 → R ). Suponha que f tem as s
Diz-se que o vetor v é combinação linear dos vetores v 1 ,v 2 ,...,v n quando se tem v=α 1 v 1+α 2 v 2+···+α n v n ,c o mα 1 ,α 2 ,...,α n∈R . Mostre que os vetores u ,vew são coplanares se, e somente
Calcule o cosseno do ângulo formado por duas diagonais de um cubo.