Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 135

Calcule a excentricidade de uma hipérbole, sabendo que as extremidades das cordas que contêm algum foco e são perpendiculares à reta focal são vértices de um quadrado.

Passo 1

Veja o esquema abaixo, onde temos a hipérbole x 2 / a 2 - y 2 / b 2 = 1 .

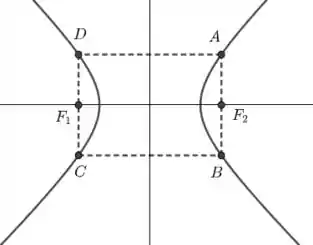
No desenho, F 1 e F 2 são focos e A B C D é um quadrado.

Passo 2

Note que a abscissa do ponto A vale c . Logo,

c 2 a 2 - y A 2 b 2 = 1 ∴ y A 2 b 2 = e 2 - 1 ⟹ y A = b e 2 - 1

Portanto, A = c ,   b e 2 - 1

Passo 3

Como A B C D é um quadrado, segue que

O F 2 - = F 2 A - ⟹ c = b e 2 - 1 ∴ c 2 = b 2 e 2 - 1

c 2 = c 2 - a 2 e 2 - 1 ∴ c 2 a 2 = c 2 a 2 - 1 e 2 - 1

e 2 = e 2 - 1 2 ⟹ e = e 2 - 1

Logo, devemos resolver a equação:

e 2 - e - 1 = 0 ⟹ e = 1 ± 5 2

Como e > 0 , segue que

e = 1 + 5 2

Resposta

Temos e = ( 1 + 5 ) / 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para as funções dadas f e g defina g / f e determine o domínio da função resultante. f x = x 2 - 9 e g x = x + 5
Para as funções dadas f e g defina g ο f e determine o domínio da função resultante. f x = x + 2 e g x = x 2 + 4
Para as funções dadas f e g defina f / g e determine o domínio da função resultante. f x = x 2 - 9 e g x = x + 5
Para as funções dadas f e g defina f ⋅ g e determine o domínio da função resultante. f x = x + 2 e g x = x 2 + 4
Para as funções dadas f e g defina f - g e determine o domínio da função resultante. f x = x 2 - 4 e g x = 4 x - 3