Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 7.Exercícios Propostos - Ex. 29

Sejam s a reta x - 9 1 = y - 2 m = z - 5 1   e π o plano 2 x   - y   +   z   - 9   =   0 .

  1. Determine m para que tenhamos s / / π .
  2. Escreva equações paramétricas da reta s ' , projeção ortogonal de s sobre π . (Faça um desenho.)
  3. Na equação da reta acima, faça m = - 1 e chame a nova reta de t . Escreva equações paramétricas da reta t ' projeção ortogonal de t sobre π .

Passo 1

  1. Fala, galera! Vamos fazer aquele básico que é parametrizar uma reta:

    2. x   =   λ   + 9

    y   = m λ   + 2

    z   = λ   + 5  

    Com isso, podemos determinar o vetor diretor dessa reta, que será v → = ( 1 , m , 1 ) .

    Agora, vamos descobrir qual o vetor normal ao plano 2 x   - y   +   z   - 9   =   0 . Isso é fácil, por comparação, temos n → = ( 2 , - 1,1 ) .

    Por fim, para que s / / π . Então, seu vetor diretor é ortogonal ao plano. Assim temos que:

    v → ⋅ n → = 0   ⇒ ( 1 , m , 1 ) ⋅ ( 2 , - 1,1 ) =   0   ⇒ 2   - m   +   1   =   0   ⇒ m   =   3 .

    Passo 2

    Bom, vamos começar considerando algumas ideias. Primeiramente, precisamos descobrir qual o ponto inicial dessa reta. Para isso, sabemos que S   =   ( λ   + 9 ,   m λ   + 2 ,   λ   + 5 ) e tomaremos o valor de λ   =   0 , para descobrir qual o ponto inicial. Assim, S   =   ( 9,2 , 5 ) .

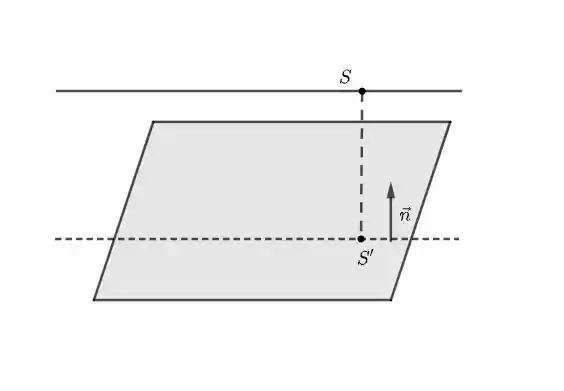
    Agora, partindo da ideia que a projeção ortogonal da reta S sobre o plano π será como se pegássemos vários segmentos projetando vetores ortogonais até o plano. Como se quiséssemos a sombra que essa reta faz no plano. Então, precisamos achar um vetor normal, em sua forma parametrizada, que nos forneça o ponto em que a reta S ' comece. Ou seja:

    n ' →     =   ( 9 ,   2,5 )   -   n → γ   = ( 9 ,   2,5 )   - ( 2 , - 1,1 ) γ   =   ( 9 - 2 γ ,   2 + γ ,   5 - γ )   ,

    Precisamos descobrir qual o valor de γ para que n ' →   cruze o plano π . Daí,

    2 ( 9 - 2 γ )   - ( 2 + γ )   + 5 - γ   - 9   =   0

    ⇒ γ ( - 4 - 1 - 1 )   + 18   - 2   + 5   - 9   =   0   ⇒   γ   =   - 12 - 6   = 2

    Substituindo   γ   =   2 em n ' → para achar o ponto desejado:

    n ' →     =   ( 9 - 2 ⋅ 2 ,   2 + 2 ,   5 - 2 )   =   ( 5,4 , 3 )

    Por fim, precisamos descobrir qual vetor diretor v s ' → = ( u , v , w ) que constrói a reta S ' e, assim, obteremos a equação paramétrica de s’.

    x   = 5   + u   t

    y   = 4   +   v t

    z   = 3   +   w t

    Passo 3

  2. Partindo do passo 2, precisamos determinar qual o vetor diretor v s ' → para o caso em que m   =   3 .

    3. Sabendo que em m   =   3 a reta s é paralela ao plano π , teremos que o vetor diretor v s ' → será o mesmo que o de v → = ( 1,3 , 1 ) . Logo, a equação paramétrica de s’ será:

    x   = 5   +   t

    y   = 4   +   3 t

    z   = 3   +   1 t

    Passo 4

  3. Partindo do passo 2, precisamos determinar qual o vetor diretor v s ' → para o caso em que m   =   - 1 .

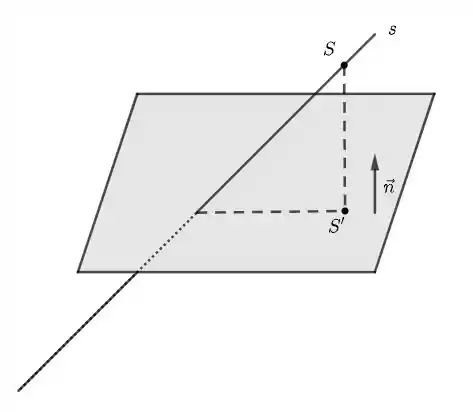
A equação paramétrica da reta T   = (   λ   + 9 , m λ   + 2 , λ   + 5 ) para m   =   - 1 será T   = (   λ   + 9 , - λ   + 2 , λ   + 5 ) . Com isso, obtemos que o seu vetor diretor é v t → = ( 1 , - 1,1 )

Agora, precisamos do ponto que a reta t intercepta o plano π . Para isso, vamos substituir os valores de x , y e z pelos da reta:

2 (   λ   + 9 )   - ( - λ   + 2 )   + λ   + 5 - 9   =   0  

⇒   λ ( 2   +   1   +   1 )   + 18   - 2   - 4   =   0   ⇒ 4 λ   =   - 12   ⇒ λ   = -   3  

Sendo λ   =   3   o parâmetro do ponto de interseção. Logo, o ponto será ( 6,5 , 2 ) .

Por fim, o vetor diretor da reta projetada, v t ' →   =   ( 6,5 , 2 )   -   ( 5,4 , 3 )   =   ( 1,1 , - 1 ) .

e as equações paramétricas da projeção t ' será:

x   = 5   +   n

y   = 4   +   n

z   = 3   - n

Resposta

  1. m   =   3 ;
  2. x   =   5   +   t , y   = 4   + 3 t , z   = 3   + t   ;
  3. x   =   5   +   n , y   = 4   + n , z   = 3   -   n   .

Exercícios de Livros Relacionados

Dados A = (1, 2, 3) e B = (4, 5, 6), determine os pontos em que a reta AB corta os planos Πxy, Πxz e Πyz.
No exercício anterior, supondo que as retas dadas sejam paralelas, que se pode dizer sobre a reta (αa1 + βa2)x + (αb1 + βb2)y = αc1 + βc2?
Na situação dos dois exercícios anteriores, diz-se que a terceira equação é combinação linear das duas primeiras. Num sistema de 3 ou mais equações a 2 incógnitas, se duas das equações representam ret
Sejam a1x + b1y = c1 e a2x + b2y = c2 retas que se intersectam no ponto P. Prove que uma reta do plano passa por P se, e somente se, sua equação é da forma (αa1 + βa2)x + (αb1 + βb2)y = αc1 + βc2 onde
Determine a interseção da reta que passa pela origem e tem vetor diretor V = i + 2j +k com o plano 2x + y + z = 5.