Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 29.Problemas - Ex. 9
Sejam AB e CD retas paralelas. Ache uma equação para o plano determinado por elas.
Passo 1
Saudações galerinha, tudo bem?
Vamos começar a resolver mais um exercício, bora lá então!
Esse exercício é bem fácil, mas é totalmente algébrico.
tá preparado ?
Suponha duas retas paralelas de equações:
e
Vamos observar o diagrama
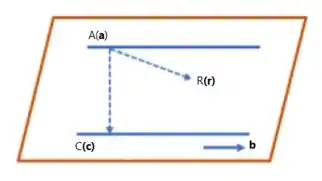
Como mostrado no diagrama, para qualquer posição de R no plano, os vetores , e são coplanares.
Então:
que é a equação necessária do plano.
Só isso galera! Essa foi fácil!
Prontinho!
Acabamos te vejo na próxima questão!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Obter uma equação geral do plano que contenha o ponto e a reta dados: A ( 3 , - 2 , - 1 ) e r : x + 2 y + z - 1 = 0 2 x + y - z + 7 = 0
Mostrar que as retas r 1 : 3 x - y - z = 0 8 x - 2 y - 3 z + 1 = 0 e r 2 : x - 3 y + z + 3 = 0 3 x - y - z + 5 = 0 São paralelas e encontrar uma equação geral do plano determinado por essas retas
Dadas as retas r 1 : y = - 2 x , z = x e r 2 : x = 2 - t , y = - 1 + t ,z = 4 - 2 t , determinar:O ponto P’ simétrico de P(1,0,5) em relação a reta r 1
Obter uma equação geral do plano que contenha o ponto e a reta dados: A ( 1,2 , 1 ) e a reta interseção do plano x - 2 y + z - 3 = 0 com o plano y O z
Dadas as retas r 1 : y = - 2 x , z = x e r 2 : x = 2 - t , y = - 1 + t ,z = 4 - 2 t , determinar:O ponto O ' simétrico de O(0,0,0) em relação a reta r 2