Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 23.Problemas - Ex. 15

uma transformação linear invertível. Mostre que transforma retas paralelas em retas paralelas, portanto paralelogramos em paralelogramos. E losangos?

Passo 1

Olá galera! tudo bem?

Bora junto resolver mais um problema!

Este exercício vai requerer um pouco mais de domínio algébrico, já que o mesmo se trata de uma demonstração.

Preparado?

Sabemos que o paralelogramo geral em pode ser descrito como , com linearmente independente e . Queremos mostrar que:

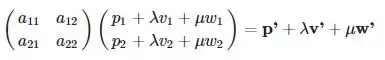
Onde são linearmente independentes.

Suponha, então,

Isso implica que:

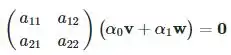
Desde é invertível, a equação tem apenas soluções triviais. Mas Porque são por definição linearmente independentes. Por isso, também é um paralelogramo.

Prontinho, acabamos te vejo na próxima questão!

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Seja T:P 2→P 3 a transformação linear definida por T p x =x p x . Em cada caso, decida se o vetor está em N u c T .Em cada caso, decida se o vetor está em N u c ( T ) . x 2 0 x + 1

Seja T:P 2→P 3 a transformação linear definida por T p x =x p x . Em cada caso, decida se o vetor está em I m T . x 2 + x x + 1 - x 2 + 3

Encontre uma base do núcleo.T (x , y) = ( 2 x - y , - 8 x + 4 y ) T (x_1 , x_2 , x_3 , x_4) = ( 4 x_1 + x_2 - 2 x_3 - 3 x_4 , 2 x_1 + x_2 + x_3 - 4 x_4 , 6 x_1 - 9 x_3 + 9 x_4 ) T (p (x)) = x p (x)

Seja T:R 4→R 3 a transformação linear dada pela fórmula T x 1 ,x 2 ,x 3 ,x 4 = ( 4 x 1 + x 2 - 2 x 3 - x 4 ,2 x 1 + x 2 + x 3 - 4 x 4 , 6 x 1 - 9 x 3 + 9 x 4 ) Em cada caso, decida se o vetor está em

Encontre uma base da Imagem.T (x , y) = ( 2 x - y , - 8 x + 4 y ) T (x_1 , x_2 , x_3 , x_4) = ( 4 x_1 + x_2 - 2 x_3 - 3 x_4 , 2 x_1 + x_2 + x_3 - 4 x_4 , 6 x_1 - 9 x_3 + 9 x_4 ) T (p (x)) = x p (x)