Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 6.Problemas propostos - Ex. 70a
Dadas as retas e , determinar:
- O ponto P’ simétrico de P(1,0,5) em relação a reta
Passo 1
Vamos começar parametrizando a reta
As equações já estão em função de , então, tomando , temos que a nossa parametrização fica:
Então nosso vetor
Passo 2
E o que seria esse ponto simétrico de em relação a reta ? é exatamente isso aqui: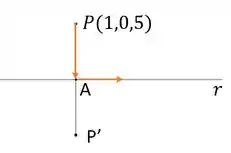 
No qual, o ponto A pertence a reta R, a distância de P até A é a mesma distancia de A até P’ e também, podemos afirmar que , onde é o vetor direção da reta .
Como o ponto A pertence a reta, chamaremos ele de
Passo 3
Então temos que , ou seja,
E
Passo 4
Como , temos que:
Resposta
Exercícios de Livros Relacionados
Determine a equação do plano.O plano que passa pelo ponto( 1,5 , 1 ) e é perpendicular aos planos 2 x + y - 2 z = 2 e x + 3 z = 4 .
Determine a equação do plano.O plano que passa pelo ponto ( 2,4 , 6 ) e é paralelo ao plano z = x + y
Determine a equação do plano.O plano que passa pelos pontos ( 0 , - 2,5 ) e ( - 1,3 , 1 ) e é perpendicular ao plano 2 z = 5 x + 4 y .
Determine a equação do plano.O plano que passa pela reta de intersecção dos planos x - z = 1 e y + 2 z = 3 e é perpendicular ao plano x + y - 2 z = 1 .
Determine a equação do plano.O plano que passa pelo ponto ( 1 , - 1 , - 1 ) e é paralelo ao plano 5 x - y - z = 6